9 Parallelograms Hiding in Plain Sight? You Won’t Believe It!
Geometry, often studied within educational institutions, isn’t confined to textbooks or classrooms. This fundamental branch of mathematics, impacting fields from architecture to art, reveals itself in unexpected ways. Consider the simple parallelogram, a quadrilateral with opposite sides parallel. You might be surprised to discover 9 everyday items that look like a parallelogram hiding in plain sight, transforming your perception of even the most mundane objects. And If you are curious to learn how Euclid would appreciate the use of parallelograms in modern architecture, continue reading!
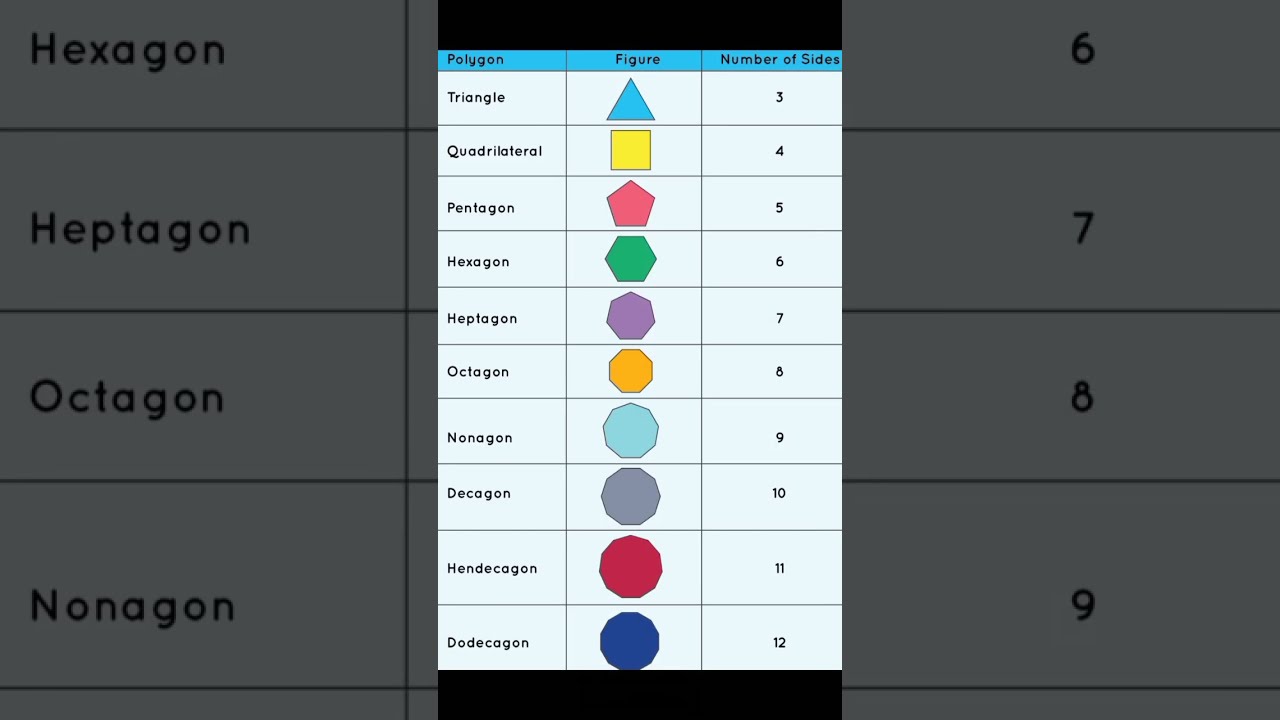
Image taken from the YouTube channel MATH CLUB , from the video titled Polygons with side up to 12 // 💁easy to remember // Math tricks 🔥 .
Did you know that the seemingly abstract world of geometry is constantly shaping your everyday experiences?
It’s true! Look around. Geometry isn’t confined to textbooks; it’s woven into the fabric of our world, often in the most unexpected places.
One shape, in particular, hides in plain sight: the parallelogram.
But what exactly is a parallelogram?
In the simplest terms, it’s a four-sided shape (a quadrilateral) with two pairs of parallel sides.
Think of a slightly slanted rectangle, and you’re on the right track.
Unveiling the Ubiquitous Parallelogram
Parallelograms are fundamental geometric shapes.
They play a crucial role in mathematics and architecture.
They are also more common in our daily lives than most people realize.
From the architecture that surrounds us to the objects we use every day, parallelograms subtly influence our visual landscape.
A Geometric Scavenger Hunt
Prepare to embark on a geometric scavenger hunt.
We’re about to reveal nine surprising everyday items that embody the principles of a parallelogram.
Get ready to see the world through a new, geometrically informed lens.
You might be surprised by how often this shape pops up when you start looking for it.
These examples showcase the versatility and prevalence of this fundamental geometric shape.
Let’s explore some fascinating real-world examples!
Parallelogram 101: A Quick Refresher
Before we dive into our geometric scavenger hunt, let’s ensure we’re all on the same page. A quick refresher on the essential characteristics of a parallelogram will help you spot them hiding in plain sight. Think of this as your parallelogram "cheat sheet".
Decoding the Parallelogram: Key Characteristics
At its core, a parallelogram is a four-sided shape, more formally known as a quadrilateral. But not just any quadrilateral qualifies! To be a parallelogram, it must possess a few defining properties.
First and foremost, opposite sides must be parallel. Parallel lines, as you might recall, are lines that run alongside each other, maintaining a constant distance and never intersecting.
Furthermore, these opposite sides aren’t just parallel, they’re also equal in length. This harmonious balance gives the parallelogram its distinctive appearance.
Finally, the opposite angles within a parallelogram are also equal. This means that the angles facing each other across the shape have the exact same measure.
The Parallelogram Family: Squares, Rectangles, and Rhombuses
Now, here’s where things get interesting. You might be thinking, "Wait a minute, that sounds a lot like other shapes I know!" And you’d be right. Squares, rectangles, and rhombuses are all special types of parallelograms.
A rectangle, for example, is a parallelogram with four right angles (90-degree angles). This added constraint makes it a specific subset of the parallelogram family.
Similarly, a rhombus is a parallelogram with all four sides equal in length. Think of it as a "tilted square".
And finally, a square is the most exclusive member of the family. It’s a parallelogram that’s both a rectangle and a rhombus – possessing four right angles and four equal sides.
Therefore, all squares, rectangles, and rhombuses are parallelograms, but not all parallelograms are squares, rectangles, or rhombuses.
Angles: The Key to Defining Parallelograms
Angles play a crucial role in defining a parallelogram and differentiating it from other quadrilaterals. The relationships between angles within a parallelogram are governed by fundamental geometric principles.
For example, the sum of adjacent angles in a parallelogram is always 180 degrees. This property stems from the fact that the parallel sides create supplementary angles when intersected by a transversal (another line).
Understanding these angular relationships is essential for calculating area, perimeter, and other properties of parallelograms. It also allows us to analyze and appreciate the geometric harmony present in designs and structures that incorporate this shape. The study of angles and their properties falls under the branch of Mathematics known as Trigonometry.
9 Everyday Parallelograms You Never Noticed
We’ve just brushed up on our parallelogram knowledge. Now, let’s put on our detective hats and uncover the surprising places these shapes are lurking in our daily lives. You might be amazed to discover how frequently parallelograms appear, often hiding in plain sight within familiar objects.
Windows: Ajar and A-Parallelogram
Take a look around your room. Is there a window? When a window is partially opened, it often transforms into a parallelogram.
The geometry of the window frame, coupled with the angle at which the window is opened, creates this shape.
The parallel sides of the frame remain parallel. The tilted angle of the open window forms the other two sides. Voila! You have a parallelogram.
Doors: Perspectives Can Be Deceiving
Similar to windows, doors can also appear as parallelograms from certain angles.
This is especially true in architecture that intentionally incorporates angled or leaning door frames.
The perspective from which you view the door can accentuate this effect.
Keep an eye out for doors that seem to subtly deviate from a perfect rectangle. You may just spot a parallelogram in disguise.
Brick Walls: Patterns in Parallel
Brick walls may seem like simple, stacked rectangles.
However, the arrangement of the bricks and the mortar lines between them often create subtle parallelogram patterns.
Look closely at how the bricks overlap in each row. You’ll notice that this offsetting can form repeating parallelogram shapes across the wall’s surface.
This is a testament to both the structural integrity and the visual design of brickwork.
Tiles: A Mosaic of Parallelograms
Tiles, especially those designed as parallelograms, offer endless possibilities for visually striking mosaics.
These shapes can be arranged to create complex patterns on both interior and exterior surfaces.
Think of tessellations, where parallelograms interlock to cover a surface without gaps.
The use of parallelogram tiles adds a dynamic and artistic element to architectural design.
Paper: Folded Geometry
A simple sheet of paper can be easily transformed into a parallelogram through folding and angling.
By making a diagonal fold across the paper and then angling the resulting shape, you can create various parallelogram designs.
This demonstrates the fundamental geometric properties inherent in even the most ordinary objects.
Experimenting with paper folding is a great way to visualize and understand parallelograms in action.
Signboards: A Shape of Attention
Signboards frequently use the parallelogram shape for aesthetic appeal.
The angled design can make the sign more eye-catching and memorable.
Parallelogram signboards can be seen in various settings, from storefronts to informational displays.
The deliberate choice of this shape adds visual interest and helps the sign stand out.
Squares: The Perfect Parallelogram
Here’s where things get interesting! A square perfectly embodies the definition of a parallelogram.
Its opposite sides are parallel and equal in length, and its opposite angles are equal (all 90 degrees!).
This means that every square is, by definition, a parallelogram. This understanding highlights the hierarchical relationship between geometric shapes.
Rhombuses: The Tilted Square
A rhombus, with all four sides equal in length, also fulfills the criteria of a parallelogram.
Its opposite sides are parallel, and its opposite angles are equal.
Think of a rhombus as a "tilted square". It’s a parallelogram with the added constraint of equal side lengths.
This reinforces the concept that specific shapes are subsets of more general categories.
Rectangles: Right Angles, Right Parallelogram
Finally, let’s consider the rectangle. A rectangle, characterized by four right angles, is also undeniably a parallelogram.
Its opposite sides are parallel and equal, and its opposite angles are equal (all 90 degrees).
The rectangle demonstrates how adding a specific condition (right angles) to a parallelogram creates a distinct, yet related, shape.
Brick walls demonstrate structural integrity through repeating parallelograms, and the doors we walk through present parallelograms from unique angles, all built on geometric principles. But beyond the visual, what mathematical truths underpin these everyday shapes?
The Underlying Mathematics: Parallelograms in Action
Parallelograms aren’t just visual curiosities; they are governed by precise mathematical rules that explain their properties and applications. Delving into the formulas and principles behind these shapes reveals a deeper understanding of their significance in both the abstract world of mathematics and the tangible world around us.
Bridging the Gap: From Observation to Calculation
The examples we’ve explored—windows, doors, brick walls, and more—all adhere to the fundamental properties of parallelograms. Opposite sides are always parallel and equal in length. Opposite angles are always equal. These aren’t just coincidences; they are the defining characteristics that allow us to apply mathematical principles to understand and analyze these shapes.
Consider a brick wall. The repeating parallelogram pattern isn’t random. It’s a result of deliberate bricklaying, adhering to geometric principles to ensure stability and visual appeal. By understanding the angles and side lengths of the parallelogram formed by the bricks, architects and builders can calculate the overall structural integrity of the wall.
Area and Perimeter: Quantifying Parallelograms
Two fundamental measurements help us quantify parallelograms: area and perimeter. The area of a parallelogram is calculated by multiplying its base by its height (Area = base × height). It’s crucial to remember that the "height" isn’t necessarily the length of one of the sides. It’s the perpendicular distance between the base and its opposite side.
The perimeter, on the other hand, is simply the sum of the lengths of all four sides. Since opposite sides of a parallelogram are equal, the formula can be simplified to Perimeter = 2 × (side 1 + side 2).
These formulas aren’t just theoretical exercises. They have practical applications in various fields. For example, calculating the area of a parallelogram-shaped tile can help determine the amount of material needed to cover a floor. Estimating the perimeter of a parallelogram-shaped signboard helps in deciding the length of decorative elements to be applied to the edges.
Parallelograms and Aesthetic Appreciation
Understanding the mathematics of parallelograms enriches our appreciation for design and architecture. When we see a window slightly ajar, forming a parallelogram, we’re not just seeing a tilted rectangle. We’re witnessing a transformation governed by geometric principles. The angle at which the window opens directly impacts the shape and area of the resulting parallelogram.
Architects and designers consciously utilize parallelograms to create visually interesting and structurally sound designs. The subtle lean of a door frame, the repeating pattern of bricks, the arrangement of tiles, all rely on an understanding of the properties of parallelograms.
By recognizing these mathematical relationships, we gain a deeper understanding of the intention and craftsmanship behind these designs. We move beyond simply seeing shapes to understanding the underlying principles that make them functional and aesthetically pleasing. We move past simply seeing to understanding.
FAQs: Finding 9 Parallelograms You Missed!
Here are some common questions about the article "9 Parallelograms Hiding in Plain Sight? You Won’t Believe It!" to help you identify these shapes around you.
What exactly is a parallelogram?
A parallelogram is a four-sided shape (quadrilateral) where opposite sides are parallel and equal in length. This means that the sides never intersect, even if extended infinitely. Think of a slightly tilted rectangle.
I’m still having trouble spotting parallelograms. Any tips?
Look for familiar shapes that have been skewed or tilted. Remember that 9 everyday items that look like a parallelogram often appear a little "off" compared to perfect rectangles or squares. Pay attention to if opposite sides are parallel.
Why does the article focus on everyday objects instead of perfect parallelograms?
The point is to show how common the parallelogram shape is in everyday life! While perfectly geometrical parallelograms are rare outside math textbooks, the "9 everyday items that look like a parallelogram" demonstrate how close many real-world objects come to that definition.
Can a rectangle or square also be a parallelogram?
Yes, absolutely! A rectangle and a square are special types of parallelograms where all angles are right angles (90 degrees). So, technically they fulfill the criteria, but the article focuses on shapes that primarily look like a "tilted" parallelogram to increase awareness of less obvious examples.
So, next time you’re looking around, keep an eye out for those 9 everyday items that look like a parallelogram! Who knew math could be so much fun?