String Tension: Mechanics Formula You NEED to Know!
Understanding tension in a string mechanics formula is crucial for professionals working with structures like suspension bridges. This formula, often explored in introductory Physics courses, allows engineers at organizations like NASA to accurately predict the forces at play in various systems. The key lies in correctly applying vector analysis and considering factors influencing the equilibrium of the string; thus, the principles, first popularized by figures like Robert Hooke in his study of elasticity, remain essential for modern structural integrity analysis.
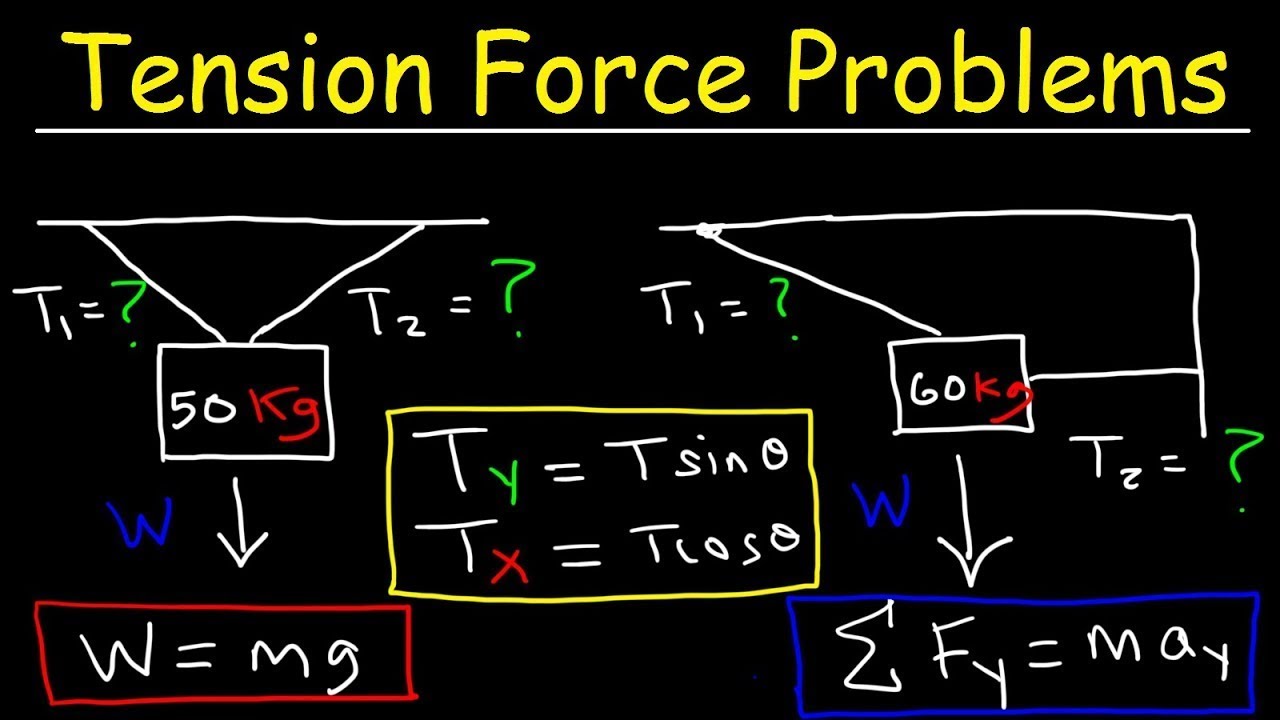
Image taken from the YouTube channel The Organic Chemistry Tutor , from the video titled Tension Force Physics Problems .
Understanding Tension in a String: A Mechanics Formula Guide
Tension, a fundamental force in mechanics, is especially crucial when dealing with strings, ropes, or cables. This guide breaks down the concept of tension, its mechanics formula, and how to apply it in practical situations.
Defining Tension and its Significance
Tension is the pulling force exerted axially by a string, cable, chain, or similar one-dimensional continuous object, or by each end of a rod or strut. It is important because it transmits force along the length of the string or cable, influencing the motion and equilibrium of connected objects.
- Axial Force: Tension acts along the longitudinal axis of the string.
- Transmission of Force: A change in tension at one point affects the tension throughout the string (assuming it’s massless and inextensible – ideal conditions).
- Equilibrium and Motion: Tension plays a critical role in balancing forces and determining the motion of objects connected by the string.
The Tension in a String Mechanics Formula Explained
The mechanics formula for tension depends on the specific scenario. However, the overarching principle involves Newton’s laws of motion, specifically the second law: F = ma, where F represents the net force, m is the mass, and a is the acceleration.
Static Equilibrium: Tension in a Stationary String
When a string is in static equilibrium (not moving), the net force acting on any point along the string is zero. This means the tension at that point must balance all other forces acting on it. Consider a simple example: a mass (m) suspended vertically by a string.
-
Forces Acting:
- Gravity (mg) acting downward on the mass.
- Tension (T) acting upward on the mass.
-
Equilibrium Condition:
- For the mass to remain stationary, the upward tension must equal the downward gravitational force: T = mg
-
Formula for Tension:
- Therefore, in this case, Tension (T) = mass (m) × acceleration due to gravity (g)
Dynamic Scenario: Tension in an Accelerating String
If the string is connected to an object that is accelerating, the tension must provide the force necessary to cause that acceleration. Consider a mass (m) being pulled horizontally across a frictionless surface by a string with tension (T), resulting in acceleration (a).
-
Forces Acting:
- Tension (T) acting horizontally on the mass.
-
Applying Newton’s Second Law:
- F = ma becomes T = ma
-
Formula for Tension:
- Therefore, in this case, Tension (T) = mass (m) × acceleration (a)
System of Masses Connected by a String
When dealing with a system of multiple masses connected by strings, the tension within each string segment may differ. This requires analyzing each mass individually and applying Newton’s second law to each.
-
Example: Two masses, m1 and m2, connected by a string passing over a frictionless pulley, with m2 hanging vertically and m1 on a frictionless horizontal surface.
-
Mass m1 (horizontal):
- Tension (T) acts horizontally, causing acceleration (a).
- T = m1 * a
-
Mass m2 (vertical):
- Tension (T) acts upward, gravity (m2 * g) acts downward, resulting in acceleration (a).
- m2 g – T = m2 a
-
Solving for Tension and Acceleration: Solving these two equations simultaneously allows you to determine the tension (T) in the string and the acceleration (a) of the system.
-
Factors Affecting String Tension
Several factors can influence the tension within a string.
- Applied Force: The magnitude of any external force applied to the string or connected objects directly affects the tension.
- Mass of the Object(s): Heavier objects require greater tension to support or accelerate them.
- Angle of the String: The angle at which the string is oriented relative to the direction of the force or gravity significantly impacts the tension. Strings pulling at angles exert less effective force in a given direction. Components of force must be considered.
- Acceleration of the System: If the object or system of objects is accelerating, the tension must account for the inertial forces.
- Friction (if present): Friction between the object and a surface opposes motion, requiring a greater tension to overcome it.
- Elasticity of the String (Real-world scenario): In reality, strings are not perfectly inextensible. The elasticity of the string introduces the concept of strain and stress, where the tension is related to the extension of the string. However, the ideal string model ignores this.
Examples and Applications of Tension in Strings
Tension is a ubiquitous concept encountered in numerous physics and engineering applications.
- Elevators: The cable supporting an elevator experiences tension due to the weight of the elevator car and its passengers.
- Bridges: Suspension bridges utilize cables under significant tension to support the weight of the bridge deck.
- Musical Instruments: The tension in guitar strings determines the pitch of the sound produced.
- Simple Machines: Pulleys use tension in ropes or cables to alter the direction and magnitude of forces.
- Sports Equipment: The strings in a tennis racket or bow and arrow experience tension when in use.
How to Calculate Tension: Step-by-Step Guide
Calculating tension typically involves the following steps:
- Draw a Free Body Diagram: Illustrate all the forces acting on the object(s) connected to the string.
- Apply Newton’s Second Law: ΣF = ma, resolving forces into their components if necessary (x and y).
- Set Up Equations: Based on the free body diagram and Newton’s second law, establish equations relating tension to other forces, mass, and acceleration.
- Solve for Tension: Solve the equations to determine the value of the tension. This may involve simultaneous equations if there are multiple unknowns.
- Check Your Answer: Ensure the units are consistent and that the answer makes logical sense in the context of the problem.
| Step | Description |
|---|---|
| 1 | Draw a Free Body Diagram |
| 2 | Apply Newton’s Second Law |
| 3 | Set Up Equations |
| 4 | Solve for Tension |
| 5 | Check Your Answer |
FAQs About String Tension & Mechanics Formulas
Here are some frequently asked questions to further clarify the concepts discussed in the article about string tension and its mechanics.
What exactly is string tension?
String tension is the pulling force exerted by a string or cable. In a static situation, it’s the force being transmitted through the string when pulled tight by forces acting from opposite ends. Understanding this is crucial for the tension in a string mechanics formula applications.
Why is knowing the tension in a string mechanics formula important?
Knowing the tension in a string is essential for calculating the forces involved in various systems, such as bridges, musical instruments, or even simple pulleys. The tension in a string mechanics formula allows you to predict how a system will behave under load and design it accordingly to prevent failure.
Does the length of the string affect the tension?
The length of the string itself doesn’t directly change the tension unless it impacts other variables in the system, like the angle of suspension or the forces applied. Tension is primarily dependent on the forces acting on the string ends, not its overall length. To accurately measure tension in a string mechanics formula, consider all connected external variables.
How does the angle of the string affect tension?
The angle at which a string is pulled has a significant impact on the tension. If the string is pulled at an angle, the tension will have both horizontal and vertical components. The greater the angle, the greater the tension required to support the same weight. This is why understanding vector components is key to applying a tension in a string mechanics formula correctly.
So, there you have it! Hopefully, you now have a better grip on tension in a string mechanics formula and can confidently tackle those physics problems. Go forth and calculate!