Unlock the Square Root Inverse: Simple Guide! 60 Char
The concept of reciprocity holds crucial significance when understanding the square root inverse. Specifically, mathematical analysis frequently employs this operation to simplify equations, especially in physics. Calculating the square root inverse benefits from tools such as scientific calculators, aiding in precise computations. These calculations are crucial in various fields of study and professional applications. Understanding these processes and tools can greatly help in grasping the square root inverse.
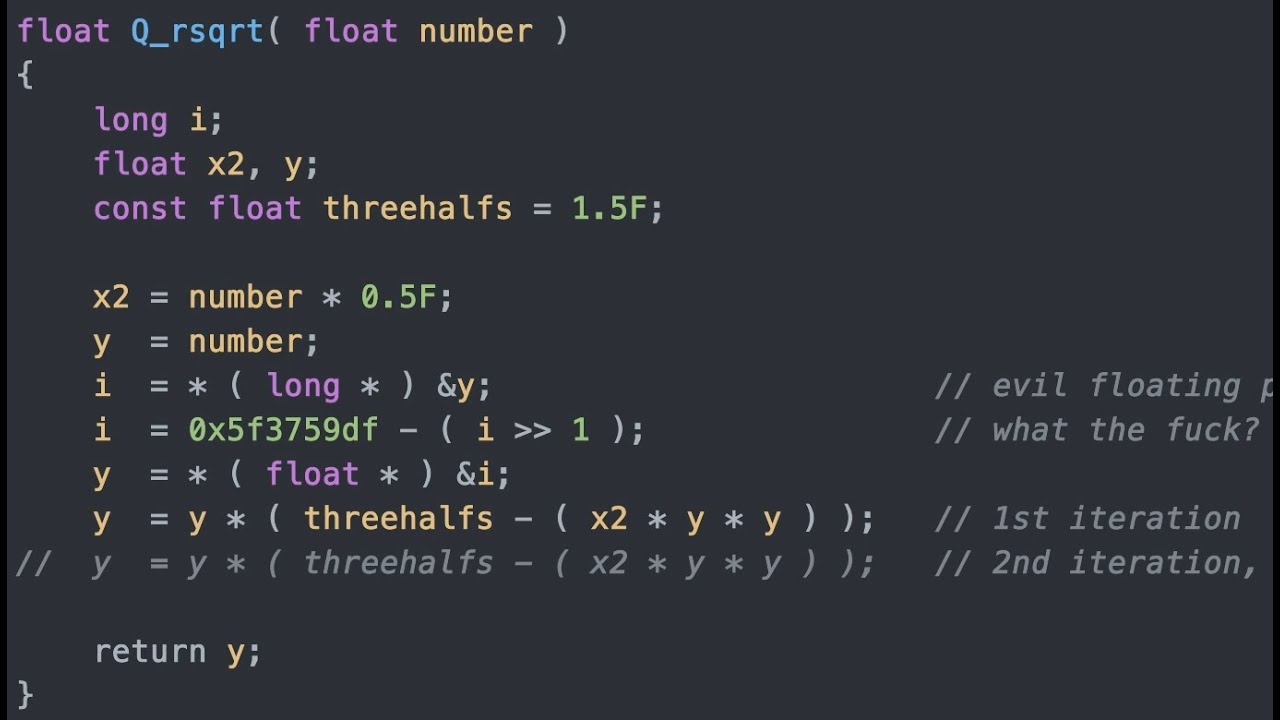
Image taken from the YouTube channel Nemean , from the video titled Fast Inverse Square Root — A Quake III Algorithm .
Unlocking the Square Root Inverse: A Simple Guide
This article aims to clearly explain the concept of the square root inverse, providing an accessible understanding for anyone, regardless of their mathematical background. We’ll break down what it is, how it works, and why it’s useful.
What is the Square Root Inverse?
The square root inverse combines two mathematical operations: finding the square root and finding the inverse (or reciprocal) of that square root. Let’s break it down further.
Square Root Explained
The square root of a number ‘x’ is a value ‘y’ that, when multiplied by itself, equals ‘x’. Mathematically, this is represented as:
y * y = x or √x = y
For example, the square root of 9 is 3, because 3 * 3 = 9.
The Inverse (Reciprocal) Explained
The inverse (or reciprocal) of a number is simply 1 divided by that number. The inverse of ‘x’ is 1/x.
For example, the inverse of 5 is 1/5, which equals 0.2.
Combining Square Root and Inverse
The square root inverse of a number ‘x’ is therefore 1 divided by the square root of ‘x’. Mathematically, this is written as:
Square Root Inverse(x) = 1 / √x
How to Calculate the Square Root Inverse
Calculating the square root inverse involves two steps:
-
Calculate the Square Root: Find the square root of the number. You can use a calculator, online tools, or estimate it manually for simpler numbers.
-
Calculate the Inverse: Divide 1 by the result of the square root you just calculated.
Let’s look at some examples:
-
Example 1: Find the square root inverse of 4.
- Step 1: √4 = 2
- Step 2: 1 / 2 = 0.5
- Therefore, the square root inverse of 4 is 0.5.
-
Example 2: Find the square root inverse of 9.
- Step 1: √9 = 3
- Step 2: 1 / 3 = 0.333… (approximately)
- Therefore, the square root inverse of 9 is approximately 0.333.
We can represent these examples in a table for better visualization:
| Number (x) | Square Root (√x) | Square Root Inverse (1/√x) |
|---|---|---|
| 4 | 2 | 0.5 |
| 9 | 3 | 0.333… |
Practical Applications of the Square Root Inverse
While the square root inverse might seem abstract, it appears in various fields:
-
Physics: It’s relevant in calculations involving wave mechanics and certain types of potential energy functions.
-
Statistics: The concept can be useful in certain statistical normalizations and transformations.
-
Engineering: Appears in equations related to impedance matching and signal processing.
The usefulness is often tied to mathematical models where the rate of change decreases proportional to 1/√x, or similar relationships. These appear regularly in applied science and engineering.
FAQs: Understanding Square Root Inverses
Here are some common questions about the square root inverse and how it works.
What exactly is the square root inverse?
The square root inverse, also known as squaring, is the opposite operation of taking the square root. It "undoes" the square root. If you take the square root of a number and then square the result, you get back the original number.
How do I calculate the square root inverse?
Calculating the square root inverse (squaring) is simple: multiply the number by itself. For example, the square root inverse of 5 is 5 * 5 = 25.
Why is understanding the square root inverse important?
It helps in solving equations where the variable is under a square root. By applying the square root inverse (squaring both sides of the equation), you can isolate the variable and find its value.
Are there any limitations to the square root inverse?
Yes, when dealing with real numbers. You can’t take the square root of a negative number and get a real number result. Also, remember squaring can sometimes introduce extraneous solutions, so always verify your answers.
So, now you’ve got a handle on the square root inverse! Go forth, conquer those equations, and impress your friends with your newfound mathematical prowess. Happy calculating!