Unlock Insights: Regression Fitted Values Demystified!
Understanding statistical modeling is crucial for deriving actionable intelligence from data, and regression fitted values play a vital role in this process. Ordinary Least Squares (OLS) regression, a fundamental technique widely used within econometrics, provides a basis for calculating these values. Researchers and data scientists at institutions like Stanford University frequently leverage regression models, and thus these values, to analyze complex relationships. Software packages like R and Python offer robust tools to compute and visualize regression fitted values, providing practical utility for interpreting model results. Therefore, mastering the interpretation of regression fitted values is paramount to unlocking the insights hidden within datasets.
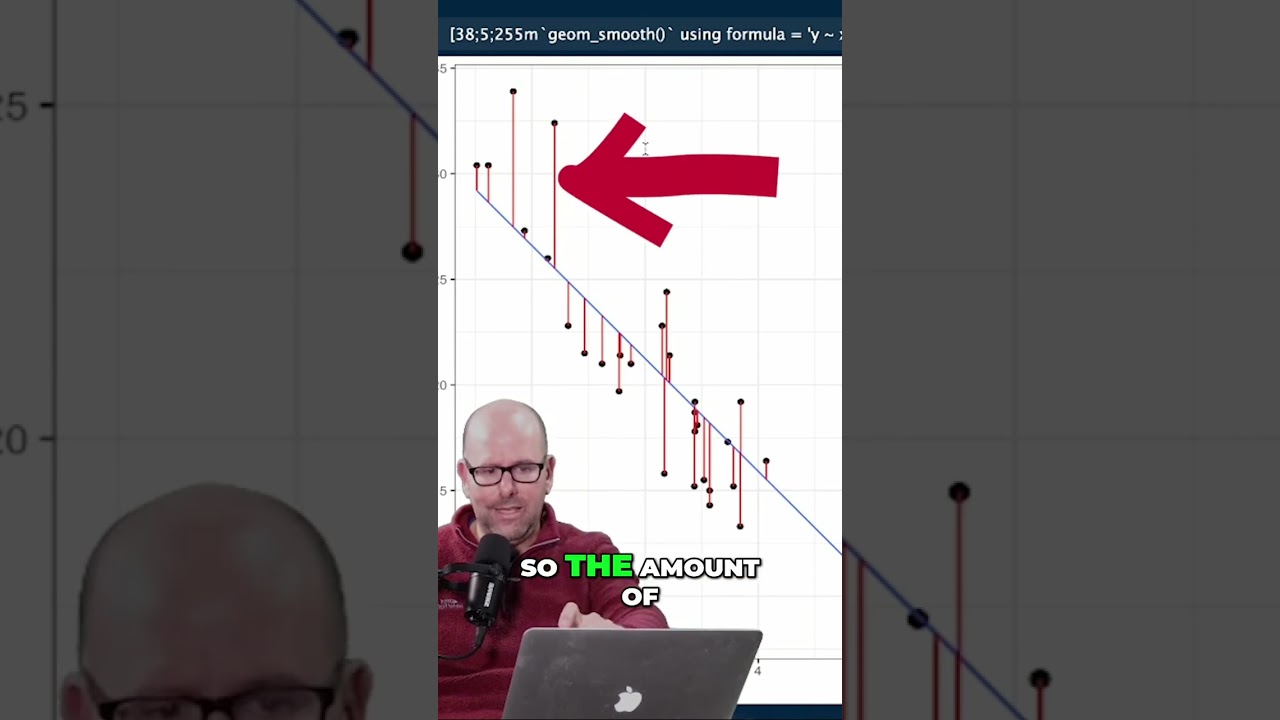
Image taken from the YouTube channel Global Health with Greg Martin , from the video titled Understanding Residuals and Fitted Values in Linear Regression .
Unlock Insights: Regression Fitted Values Demystified!
This article provides a comprehensive understanding of regression fitted values, their significance in regression analysis, and how to interpret them effectively.
What are Regression Fitted Values?
Regression fitted values, also known as predicted values, are the estimated values of the dependent variable (the variable you are trying to predict) based on the regression equation and the observed values of the independent variable(s) (the variable(s) used to make the prediction). They represent the points that lie on the regression line or surface. In simpler terms, if you plug the values of your independent variable(s) into your regression equation, the resulting output is the fitted value.
Understanding the Calculation
The process involves:
-
Building a Regression Model: This means finding the best-fitting line (or higher-dimensional surface) that describes the relationship between your independent and dependent variables. The regression model is expressed as an equation. For example, in a simple linear regression with one independent variable (X) and one dependent variable (Y), the equation might look like this: Y = a + bX, where ‘a’ is the intercept and ‘b’ is the slope.
-
Inputting Independent Variable Values: Once you have the regression equation, you substitute the actual observed values of the independent variable(s) (X) into the equation.
-
Calculating the Fitted Value: The result of the calculation is the fitted value (Ŷ or Y-hat), which represents the predicted value of the dependent variable (Y) for that specific set of independent variable values.
Difference between Fitted Values and Observed Values
It is crucial to understand that fitted values are estimates, and they will rarely perfectly match the actual observed values of the dependent variable. The difference between the observed value and the fitted value is called the residual. These residuals are a key component in assessing the quality of the regression model.
- Observed Values: The actual data points you collected for your dependent variable.
- Fitted Values: The values predicted by the regression model.
- Residuals: The difference between observed and fitted values (Observed – Fitted).
Why are Regression Fitted Values Important?
Regression fitted values offer several key benefits in understanding and evaluating your regression model.
Model Evaluation
Fitted values play a central role in assessing the accuracy and validity of the regression model.
-
Residual Analysis: Examining the pattern of residuals (the difference between observed and fitted values) can reveal potential problems with the model, such as non-linearity, heteroscedasticity (unequal variance of errors), or outliers.
- A random scatter of residuals suggests a well-fitting model.
- A pattern in the residuals suggests the model may be missing something or not adequately capturing the relationship between the variables.
-
Goodness of Fit Metrics: Fitted values are used in calculating various goodness-of-fit metrics, such as R-squared. R-squared represents the proportion of variance in the dependent variable that is explained by the independent variable(s) in the model. Fitted values are a core component in calculating the explained variance.
Prediction and Inference
Fitted values provide the basis for making predictions about the dependent variable for new values of the independent variable(s).
-
Predictive Modeling: Once the model is validated, it can be used to predict the value of the dependent variable for new data points. The fitted value is the predicted value.
-
Understanding Relationships: By examining how the fitted values change as the independent variables change, you can gain a better understanding of the relationships between the variables.
Identifying Outliers and Influential Points
Fitted values help in identifying outliers, which are data points that deviate significantly from the expected pattern.
-
Large Residuals: Outliers often have large residuals, indicating that the model does a poor job of predicting their values. These points can disproportionately influence the regression model and should be investigated.
-
Influential Points: Some data points might not be outliers in terms of their residual size, but they can still have a significant impact on the estimated regression coefficients and fitted values. Examining the influence of individual points is important for ensuring the robustness of the model.
Interpreting Regression Fitted Values
Interpreting fitted values requires understanding the context of the regression model and the variables involved.
Context Matters
The interpretation of fitted values is always in relation to the specific problem and variables being analyzed. For example:
-
If you are predicting house prices based on square footage, the fitted value represents the predicted price of a house with a specific square footage, according to your model.
-
If you are predicting customer spending based on advertising expenditure, the fitted value represents the predicted spending for a given level of advertising.
Range of Fitted Values
It’s important to consider the range of the fitted values. The fitted values should be within a reasonable range, given the context of the problem. If the model is producing fitted values that are outside the plausible range, it suggests the model may be misspecified or unreliable.
Using Fitted Values to Visualize the Regression Line/Surface
Fitted values, when plotted against the independent variables, effectively show the regression line or surface. This visualization helps understand the relationship between the variables and assess how well the model fits the data.
-
Scatter Plot with Regression Line: In simple linear regression, plotting the observed data points along with the fitted values (connected by a line) provides a visual representation of the regression model’s fit.
-
3D Scatter Plot with Regression Plane: In multiple regression with two independent variables, a 3D scatter plot showing observed data points and the regression plane (represented by the fitted values) can be used to visualize the model’s fit.
Practical Example
Let’s say we want to predict a student’s exam score (Y) based on the number of hours they studied (X). We build a simple linear regression model and find the following equation:
Y = 50 + 5X
Now, if a student studied for 10 hours (X = 10), the fitted value (Ŷ) would be:
Ŷ = 50 + 5 * 10 = 100
This means the regression model predicts that a student who studies for 10 hours will score 100 on the exam. If the student actually scored 95, the residual would be 95 – 100 = -5.
Common Mistakes to Avoid
- Over-interpreting Fitted Values: Fitted values are predictions based on the model. They are not guaranteed to be accurate and should be interpreted with caution.
- Ignoring Residual Analysis: Failing to analyze the residuals can lead to overlooking problems with the model, such as non-linearity or heteroscedasticity.
- Extrapolating Beyond the Data Range: The model is only valid within the range of the data used to build it. Extrapolating fitted values beyond this range can lead to unreliable predictions.
FAQs: Regression Fitted Values Demystified
Here are some frequently asked questions to help you better understand regression fitted values.
What exactly are regression fitted values?
Regression fitted values, also known as predicted values, are the outputs you get when you plug the values of your independent variables into the regression equation. They represent the model’s best estimate of the dependent variable for each observation in your dataset.
How do fitted values differ from the actual observed values?
Fitted values are predictions made by the regression model. They are not the actual observed values of the dependent variable. The difference between the actual and fitted values is called the residual.
What do regression fitted values tell us about the model’s performance?
By comparing fitted values to the actual values, we can assess how well the regression model fits the data. A good fit means the fitted values are close to the actual values, indicating the model is accurately predicting the dependent variable. Large differences suggest the model may not be appropriate or may be missing important variables.
Why are regression fitted values useful?
Regression fitted values are useful for visualizing the relationship between variables and identifying potential outliers. They can also be used for prediction on new data points, enabling us to estimate the dependent variable for observations not included in the original dataset.
Hopefully, this demystified regression fitted values for you! Now go forth and start making some data-driven magic happen!