Unlocking Quadratic Sum Meaning: A Simple Explanation
The Sigma Notation, a notational tool in mathematical analysis, offers a concise representation of series, and its application extends to understanding quadratic sum meaning. Statistics, particularly in variance calculations, relies heavily on the concept of squaring values and summing them. Khan Academy provides accessible educational resources that demystify complex mathematical principles, including those underpinning quadratic sum meaning. A firm grasp on Algebra, especially manipulating and interpreting equations, is fundamental for anyone seeking a thorough understanding of quadratic sum meaning.
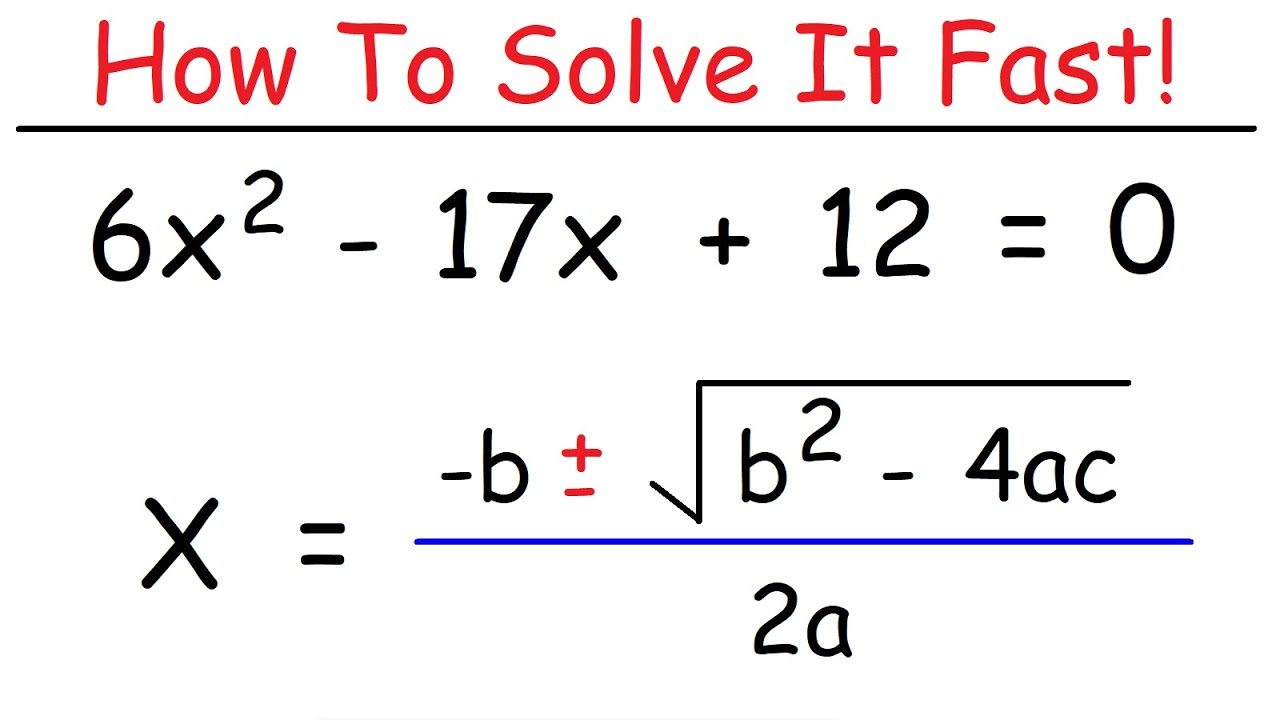
Image taken from the YouTube channel The Organic Chemistry Tutor , from the video titled How To Solve Quadratic Equations Using The Quadratic Formula .
Unlocking Quadratic Sum Meaning: A Simple Explanation
Understanding "quadratic sum meaning" requires breaking down the concept into its constituent parts and then reassembling them with clarity. We aim to achieve this by providing a structured explanation that gradually builds the reader’s understanding.
What is a Quadratic?
Before diving into the sum, let’s define the foundation: the quadratic.
- General Form: A quadratic expression usually takes the form ax² + bx + c, where ‘a’, ‘b’, and ‘c’ are constants, and ‘x’ is a variable. The key characteristic is the x² term, which is why it’s "quadratic" (related to squaring).
- Simple Examples:
- x²
- 2x² + 3x – 1
- -x² + 5
- Not Quadratic:
- x (linear)
- x³ (cubic)
- 1/x (rational)
Understanding Summation
The term "sum" simply refers to the result of adding a series of numbers. Summation is often represented using sigma notation (Σ), but for the sake of simplicity, we’ll express it in plain English for this explanation.
- Example: The sum of the numbers 1, 2, and 3 is 1 + 2 + 3 = 6.
Combining Quadratic and Sum: Defining Quadratic Sum
The core of "quadratic sum meaning" is revealed when we combine the concepts of quadratic expressions and summation. A quadratic sum involves adding together a series of terms where each term contains a quadratic expression, and this summation depends on the number of terms within that expression.
Different forms of "Quadratic Sum"
We can encounter "quadratic sum" in varying contexts, each slightly modifying its precise meaning. It’s important to distinguish these different forms.
- Sum of Squared Values: This is perhaps the most common interpretation. Here, you sum the squares of a set of numbers.
- Example: If we have the numbers 1, 2, and 3, the sum of their squares is 1² + 2² + 3² = 1 + 4 + 9 = 14.
- Sum of Terms in a Quadratic Sequence: A quadratic sequence is one where the differences between consecutive terms are not constant, but the differences of those differences are constant. Calculating the sum of the first ‘n’ terms of such a sequence constitutes a quadratic sum.
Example of Sum of Squared Values (More Detailed)
Let’s expand on the "sum of squared values" with a numerical example.
Suppose we have the data set: {4, 6, 8, 10}
- Square each value:
- 4² = 16
- 6² = 36
- 8² = 64
- 10² = 100
- Sum the squared values: 16 + 36 + 64 + 100 = 216
Therefore, the quadratic sum (specifically, the sum of squared values) for the data set {4, 6, 8, 10} is 216.
Applications of Quadratic Sums
Understanding quadratic sums is crucial in various fields:
- Statistics: Sum of squares is fundamental in variance and standard deviation calculations.
- Regression Analysis: Finding the "best fit" line often involves minimizing the sum of squared errors.
- Physics: Energy calculations frequently involve squared terms.
- Computer Science: Optimization algorithms may rely on minimizing a cost function containing a quadratic sum component.
Representing Quadratic Sum with a Formula
For a dataset x₁, x₂, …, xₙ, the quadratic sum (specifically the sum of squares) can be represented as:
∑ (xᵢ)² (from i=1 to n)
This simply means: x₁² + x₂² + … + xₙ²
Alternatively, we can consider a general term xᵢ = aᵢ² + bᵢ. The quadratic sum over n terms would be:
∑ (aᵢ² + bᵢ) (from i=1 to n)
This expands to: (a₁² + b₁) + (a₂² + b₂) + … + (aₙ² + bₙ).
Distinguishing Quadratic Sum from other Types of Sums
It’s easy to confuse "quadratic sum meaning" with other related concepts. Here’s a quick comparison:
| Type of Sum | Description | Example |
|---|---|---|
| Linear Sum | Sum of numbers directly | 1 + 2 + 3 = 6 |
| Sum of Squares | Sum of each number squared | 1² + 2² + 3² = 14 |
| Sum of Cubes | Sum of each number cubed | 1³ + 2³ + 3³ = 36 |
| Arithmetic Sum | Sum of an arithmetic series (constant difference between terms) | 2 + 4 + 6 + 8 = 20 (difference of 2) |
FAQs: Understanding Quadratic Sums
Hopefully, this section addresses common questions about understanding the quadratic sum meaning discussed in this article.
What exactly is a quadratic sum?
A quadratic sum involves adding terms where each term is a variable squared. This concept is key to understanding its application in optimization problems and statistical analysis.
Why are quadratic sums important?
Quadratic sums appear frequently in various mathematical and scientific fields. Recognizing them helps in simplifying equations and finding solutions in contexts like least squares and minimizing errors.
How does a quadratic sum relate to optimization?
The quadratic sum meaning often plays a crucial role in finding the minimum or maximum value of a function. Many optimization techniques rely on minimizing or maximizing expressions containing quadratic sums.
Can you give a simple real-world example?
Imagine trying to fit a curve to a set of data points. The goal might be to minimize the sum of the squared distances between the curve and the points. This minimization problem directly involves understanding quadratic sum meaning.
So, hopefully, this breakdown clears things up and you now have a solid handle on quadratic sum meaning! Go forth and conquer those equations!