Population Mean vs. Statistic: You Won’t Believe This!
In statistical analysis, the population mean represents a crucial parameter, indicating the average value across an entire group, while a statistic, such as the sample mean, provides an estimate derived from a subset of that population. Understanding their relationship is vital, especially when exploring concepts like the Central Limit Theorem, which connects sample statistics to the population mean. The question of is the population mean a statistic is often debated, considering the role of inferential statistics, where we use sample data to make inferences about the larger population.
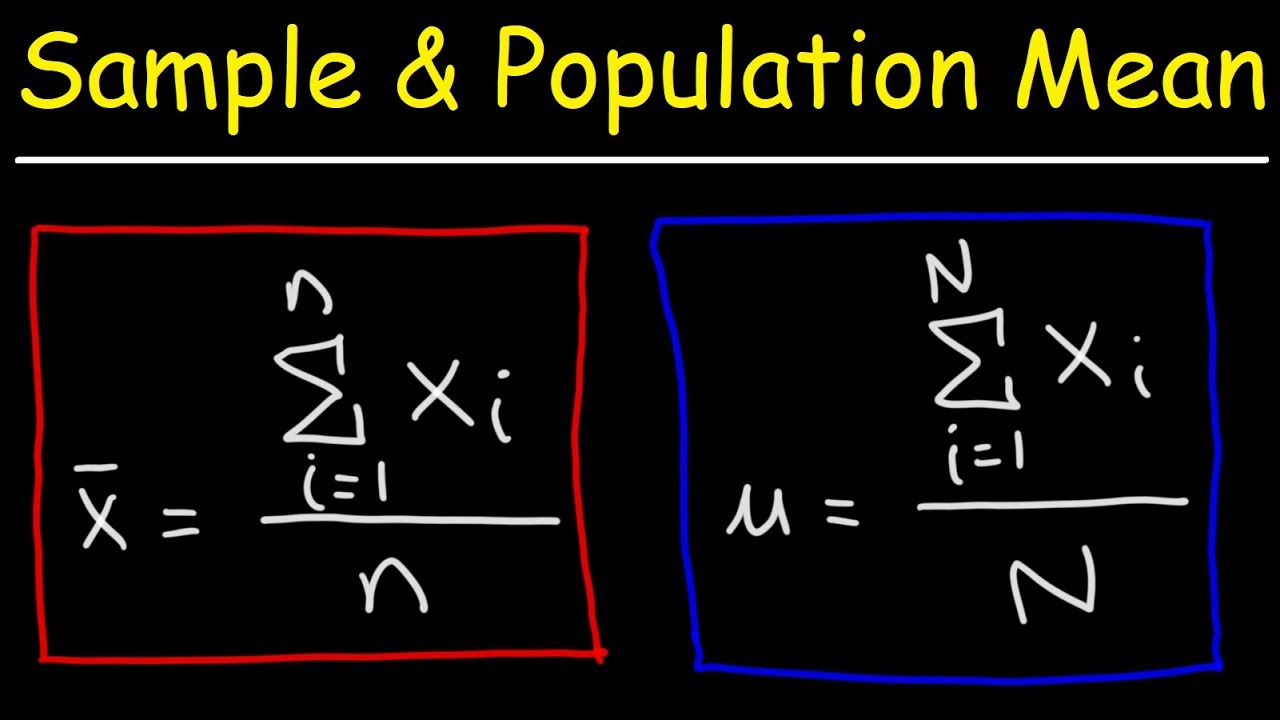
Image taken from the YouTube channel The Organic Chemistry Tutor , from the video titled Sample Mean and Population Mean – Statistics .
Unpacking Population Mean and Statistics: Is the Population Mean a Statistic?
The question "is the population mean a statistic?" reveals a common source of confusion in statistics. This article aims to clarify the differences between population parameters, like the population mean, and sample statistics. It will explore why the population mean itself is not a statistic, but is instead a key parameter that statistics are used to estimate.
Defining Population and Sample
To understand why the population mean isn’t a statistic, it’s essential to first define the concepts of a population and a sample.
What is a Population?
A population refers to the entire group of individuals, objects, or measurements of interest in a study. It’s the complete set from which data could theoretically be collected. For example:
- All registered voters in a country.
- Every tree in a forest.
- The total number of lightbulbs produced by a factory in a year.
What is a Sample?
A sample is a subset of the population selected for analysis. Because studying an entire population is often impractical or impossible, researchers collect data from a representative sample and use it to draw inferences about the population. Examples include:
- A random selection of 1000 registered voters to gauge public opinion.
- Measuring the height of 50 randomly chosen trees to estimate the average tree height in the forest.
- Testing 100 lightbulbs to assess the overall quality of the factory’s output.
Parameters vs. Statistics: The Crux of the Matter
The distinction between a population mean and a statistic relies on the difference between population parameters and sample statistics.
Population Parameters: Describing the Whole
A population parameter is a numerical value that describes a characteristic of the entire population. Because it’s based on the entire population, its value is usually unknown and fixed. Common population parameters include:
- Population Mean (μ): The average value of a variable for the entire population.
- Population Standard Deviation (σ): A measure of the spread or variability of data around the population mean.
- Population Proportion (P): The proportion of the population that possesses a certain characteristic.
Crucially, the population mean (μ) is a parameter, not a statistic. It’s a fixed value representing the true average of the entire population.
Sample Statistics: Estimating from a Subset
A sample statistic is a numerical value that describes a characteristic of a sample. Statistics are calculated from sample data and are used to estimate population parameters. Because they are based on a sample, statistics can vary from sample to sample. Examples include:
- Sample Mean (x̄): The average value of a variable calculated from a sample. It estimates the population mean (μ).
- Sample Standard Deviation (s): A measure of the spread of data around the sample mean. It estimates the population standard deviation (σ).
- Sample Proportion (p): The proportion of a sample that possesses a certain characteristic. It estimates the population proportion (P).
Therefore, a sample mean is a statistic, while the population mean is a parameter that the sample mean attempts to estimate.
Why is the Population Mean Not a Statistic?
The fundamental reason the population mean (μ) is not a statistic is that it is a characteristic of the entire population, not a sample.
Consider these points:
-
Calculation: The population mean is, in theory, calculated using data from every single member of the population. A statistic, on the other hand, is always calculated from a subset of the population.
-
Estimation: Statistics are used to estimate population parameters. If the population mean were a statistic, it would be estimating itself, which is logically inconsistent.
-
Variability: Statistics vary from sample to sample. If we take different samples from the same population, we’ll likely get slightly different values for the sample mean, sample standard deviation, etc. However, the population mean (μ) remains constant (assuming the population doesn’t change). It’s a fixed value.
Illustrative Table
| Feature | Population Parameter (e.g., Population Mean μ) | Sample Statistic (e.g., Sample Mean x̄) |
|---|---|---|
| Based on | Entire Population | Sample from the Population |
| Value | Typically Unknown, Fixed | Known (Calculated from Sample), Variable |
| Purpose | Describes the Population | Estimates Population Parameter |
| Variability | None | Varies from Sample to Sample |
Example Scenario
Imagine you want to know the average height of all adult women in a country.
- Population: All adult women in that country.
- Population Mean (μ): The true average height of all adult women in the country. This is a population parameter, and we likely don’t know its exact value.
- Sample: You randomly select 500 adult women and measure their heights.
- Sample Mean (x̄): The average height calculated from your sample of 500 women. This is a sample statistic.
- You use the sample mean (x̄) to estimate the population mean (μ). Because you didn’t measure every woman in the country, your sample mean is an estimate, not the true population mean.
Population Mean vs. Statistic: Frequently Asked Questions
Here are some frequently asked questions to clarify the difference between population means and statistics.
What’s the main difference between a population mean and a statistic?
The population mean is the true average of a characteristic for the entire group you’re interested in. A statistic is a calculated value, like an average, taken from a sample of that population. Statistics are used to estimate population parameters.
Why can’t we always know the population mean directly?
Often, it’s simply impossible or impractical to collect data from every single member of a population. Think about trying to survey every adult in a country, or measuring the lifespan of every lightbulb produced by a factory.
So, is the population mean a statistic?
No, the population mean is not a statistic. It’s a parameter. A statistic is a value calculated from a sample and used to estimate the population mean (or other population parameters).
How accurate are statistics at estimating the population mean?
The accuracy of a statistic in estimating the population mean depends on several factors, including sample size and how representative the sample is of the population. Larger, more representative samples generally lead to more accurate estimates.
So, what do you think? Did we clear up the confusion about whether is the population mean a statistic? Hopefully, you’re now armed with the knowledge to confidently tackle those stats problems. Keep exploring and happy analyzing!