Decode Paris’ Law: Fatigue Life Prediction Secrets!
Fatigue crack growth, a critical concern in structural integrity, is accurately modeled by Paris’ Law. This law, an empirical relationship, offers a powerful framework for predicting the fatigue life of components, especially within industries heavily reliant on cyclical loading. ASTM standards provide the standardized testing methodologies to determine the material constants required for applying paris law for predicting fatigue life. Accurate application can even mitigate risks of component failure and improve design in the long run, and leading engineers often utilize advanced simulations, like those offered by ANSYS, to further refine predictions based on Paris’ Law when considering complex geometries and loading conditions, thereby optimizing material science.
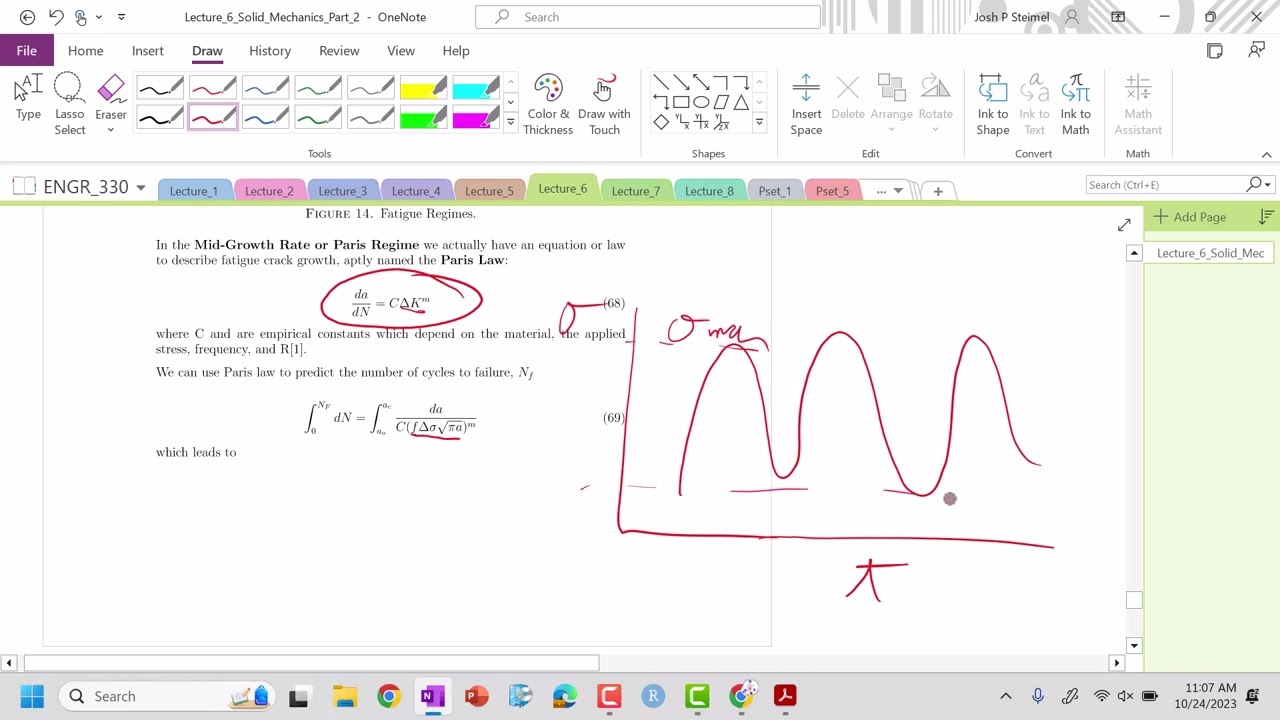
Image taken from the YouTube channel Dr. Joshua Paul Steimel , from the video titled Lecture 6: Fatigue and Paris Law .
Decoding Paris’ Law: Unveiling Fatigue Life Prediction Secrets
Paris’ Law, a cornerstone in the field of fracture mechanics, offers a powerful method for predicting the fatigue life of materials under cyclic loading. Understanding and effectively applying this law can significantly improve the durability and reliability of engineering structures. This explanation will delve into the intricacies of Paris’ Law, focusing on its application in paris law for predicting fatigue life.
Understanding Fatigue and Crack Growth
Before exploring Paris’ Law, it’s crucial to understand the underlying concept of fatigue. Fatigue is the progressive and localized structural damage that occurs when a material is subjected to cyclic loading. This loading can be well below the material’s yield strength. Over time, this cyclic stress leads to the initiation and propagation of cracks, ultimately leading to failure.
Stages of Fatigue Failure
- Crack Initiation: Small cracks form at stress concentrations, such as notches or surface imperfections.
- Crack Propagation: These cracks gradually grow larger with each loading cycle. This is where Paris’ Law becomes highly relevant.
- Final Fracture: The crack reaches a critical size, leading to sudden and catastrophic failure.
Introducing Paris’ Law
Paris’ Law describes the relationship between the crack growth rate and the stress intensity factor range. It’s primarily used to predict the crack propagation stage of fatigue life.
The Paris’ Law Equation
The mathematical representation of Paris’ Law is:
da/dN = C (ΔK)^m
Where:
da/dNrepresents the crack growth rate per cycle (e.g., mm/cycle, in/cycle).ΔKrepresents the stress intensity factor range. This is the difference between the maximum and minimum stress intensity factors during a loading cycle.Candmare material constants. These constants are determined experimentally for each specific material and environment.
Deciphering the Parameters
Let’s break down each parameter to better understand its significance:
- Crack Growth Rate (da/dN): This tells us how much the crack extends with each load cycle. A higher value means faster crack growth and a shorter fatigue life.
- Stress Intensity Factor Range (ΔK): This reflects the stress concentration at the crack tip during each cycle. A higher ΔK accelerates crack growth. It’s influenced by the applied stress range, the crack size, and the geometry of the component.
- Material Constants (C and m): These are empirical constants obtained from laboratory tests. They are highly dependent on the material’s composition, microstructure, temperature, and the environment in which it operates. The value of ‘m’ is particularly important, as it determines the sensitivity of crack growth rate to changes in ΔK.
Applying Paris’ Law for Predicting Fatigue Life
The primary application of Paris’ Law is paris law for predicting fatigue life. This involves integrating the Paris’ Law equation over the crack size range of interest.
Steps in Fatigue Life Prediction
-
Determine Material Properties: Obtain the values of C and m for the material under consideration from experimental data or material databases. Consider the specific environmental conditions and loading frequency.
-
Define Initial Crack Size (a₀): Estimate or measure the initial crack size. This is often based on the detection capabilities of non-destructive testing methods.
-
Define Critical Crack Size (ac): Determine the crack size at which failure is expected to occur. This is usually based on fracture toughness considerations.
-
Calculate ΔK as a Function of Crack Size (a): This is often the most complex step, as it requires accurate stress analysis. The stress intensity factor range (ΔK) depends on the applied stress range, the geometry of the component, and the crack size. Numerous handbooks and software tools can assist in calculating ΔK.
-
Integrate Paris’ Law: Integrate the Paris’ Law equation from the initial crack size (a₀) to the critical crack size (ac) to obtain the number of cycles (N) required for the crack to grow to failure.
N = ∫(da / (C (ΔK(a))^m)) from a₀ to a<sub>c</sub>Where:
- N represents the number of cycles to failure.
- The integral is evaluated from the initial crack size (a₀) to the critical crack size (ac).
- ΔK(a) denotes the stress intensity factor range as a function of crack size.
-
Consider Load Spectrum Effects: In real-world applications, the loading is often not constant amplitude. Account for variable amplitude loading using cycle counting methods like rainflow counting and incorporate appropriate damage accumulation models (e.g., Miner’s rule).
Considerations and Limitations
- Paris’ Law is most accurate in the mid-range of crack growth rates. It’s less accurate near the threshold stress intensity factor range (ΔKth), where crack growth is very slow or non-existent, and near the critical stress intensity factor (Kc), where crack growth becomes unstable.
- The accuracy of the prediction depends heavily on the accuracy of the material properties (C and m) and the calculation of the stress intensity factor range (ΔK).
- Residual stresses, corrosion, and other environmental factors can significantly affect fatigue life and may need to be considered in the analysis.
Example Calculation
Let’s illustrate with a simplified example:
Assume:
- Material: Aluminum Alloy 2024-T3
- C = 1.0 x 10-11 (units depend on ΔK and da/dN)
- m = 3
- Initial Crack Size (a₀) = 1 mm
- Critical Crack Size (ac) = 10 mm
- ΔK = 10 MPa√m (Assuming this remains constant for simplicity, which is rarely the case in reality)
Then, the number of cycles (N) can be approximated as:
N ≈ (1 / (C (ΔK)m)) (ac – a₀) = (1 / (1.0 x 10-11 (10)3)) (10 mm – 1 mm) = 9,000,000 cycles
This simplified example illustrates the basic principle. In practice, more complex numerical integration methods and variable ΔK values are typically required. This example is for demonstration purposes only. Proper calculations for real-world scenarios will require professional engineering analysis.
FAQs: Decode Paris’ Law – Fatigue Life Prediction Secrets!
This section answers common questions about Paris’ Law and its application in fatigue life prediction. We aim to provide clear and concise explanations for better understanding.
What exactly does Paris’ Law predict?
Paris’ Law is used for predicting fatigue life, specifically the crack growth rate in a material under cyclic loading. It describes how quickly a crack will propagate based on the stress intensity factor range. It doesn’t predict total life but rather the stable crack growth portion.
How is Paris’ Law used for predicting fatigue life in engineering?
Engineers use Paris’ Law to estimate the remaining life of a component with an existing crack or to design components to withstand a certain number of cycles before failure. By knowing the initial crack size, stress range, and material properties, we can apply paris law for predicting fatigue life.
What are the limitations of Paris’ Law?
Paris’ Law is most accurate in the mid-range of crack growth rates. It’s less reliable near the threshold stress intensity (where cracks barely grow) and near final fracture. Environmental factors and complex loading conditions can also affect its accuracy, making paris law for predicting fatigue life less straightforward.
What parameters are needed to apply Paris’ Law effectively?
To use Paris’ Law effectively, you need the stress intensity factor range (ΔK), the crack length (a), and the Paris’ Law material constants (C and m). These constants are typically determined experimentally for a given material and environment. With those values, we can apply paris law for predicting fatigue life.
So, that’s a wrap on decoding Paris’ Law! Hopefully, you’ve got a better handle on using paris law for predicting fatigue life. Time to put that knowledge to work and see what you can build (or prevent from breaking!).