Legs & Hypotenuse: Unlocking the Right Triangle’s Secret
Understanding the fundamental relationship between the legs and hypotenuse of a right triangle is crucial for anyone venturing into geometry and beyond. This relationship, elegantly captured by the Pythagorean Theorem, allows us to calculate unknown side lengths when we know others. Euclid’s meticulous work in ‘The Elements’ provides the foundational axioms upon which our understanding of right triangles rests. The practical applications of this knowledge are vast, from architectural design to GPS navigation. And finally, software tools such as GeoGebra allow students and professionals alike to visualize and manipulate right triangles, thus solidifying their understanding of how legs and hypotenuse are fundamentally linked.
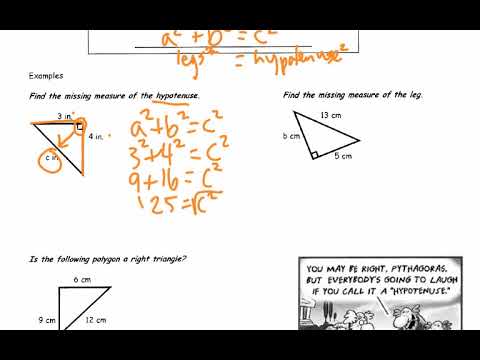
Image taken from the YouTube channel Kayla Brimlow , from the video titled Finding Missing Legs & Hypotenuse .
Legs & Hypotenuse: Crafting the Ideal Article Layout
To effectively explain the relationship between the legs and hypotenuse of a right triangle, the article layout should prioritize clarity and logical progression. Here’s a proposed structure, optimized for understanding and incorporating the main keyword "legs and hypotenuse":
I. Introduction: Setting the Stage
The introduction should grab the reader’s attention and clearly define the scope of the article.
- Hook: Start with a relatable scenario (e.g., calculating the distance diagonally across a rectangular field) or a historical anecdote (e.g., referencing early surveying techniques).
- Define a Right Triangle: Briefly explain what constitutes a right triangle – a triangle with one angle measuring exactly 90 degrees.
- Introduce Legs and Hypotenuse: Clearly define the terms "legs" and "hypotenuse" in the context of a right triangle. Highlight that the hypotenuse is always opposite the right angle. Include a simple diagram labeling the legs and hypotenuse.
- Article Overview: Briefly state what the article will cover, hinting at the relationship between the legs and hypotenuse (Pythagorean theorem).
II. Defining "Legs and Hypotenuse" in Detail
This section delves deeper into the characteristics of each component, solidifying the reader’s understanding.
A. Understanding the "Legs"
- Definition Revisited: Reiterate the definition of the legs as the two sides that form the right angle.
- Visual Representation: Use multiple diagrams showing various right triangles with the legs clearly labeled. Consider varying the orientation of the triangle to avoid the misconception that the legs are always vertical and horizontal.
- Alternative Terminology: Briefly mention if there are alternative terms used for the legs (e.g., "cathetus").
B. Delving into the "Hypotenuse"
- Definition and Identification: Reinforce the hypotenuse as the side opposite the right angle and the longest side of the right triangle.
- Uniqueness: Emphasize that a right triangle has only one hypotenuse.
- Hypotenuse vs. Other Sides: Explain why the hypotenuse is always the longest side. This can be touched upon without directly referencing the Pythagorean theorem at this point.
III. The Pythagorean Theorem: Unveiling the Relationship
This is the core of the article, where the relationship between the legs and hypotenuse is formally introduced.
A. Statement of the Theorem
- Formal Definition: State the Pythagorean Theorem: a² + b² = c², where ‘a’ and ‘b’ are the lengths of the legs, and ‘c’ is the length of the hypotenuse.
- Clear Variable Explanation: Explicitly define what ‘a’, ‘b’, and ‘c’ represent in the context of the legs and hypotenuse.
- Visual Aid: Include a diagram illustrating a square built on each side of the right triangle, visually demonstrating the relationship between the areas.
B. Applying the Theorem: Examples
- Simple Numerical Examples: Provide several worked-out examples showing how to calculate the length of the hypotenuse when the lengths of the legs are known, and vice versa.
- Step-by-Step Explanation: Break down each step of the calculation process clearly.
- Variations: Show examples where the length of one leg needs to be calculated when the hypotenuse and the other leg are known.
-
Example Table:
Leg a Leg b Hypotenuse c Calculation 3 4 ? 3² + 4² = c² ; c = 5 5 ? 13 5² + b² = 13² ; b = 12 ? 8 10 a² + 8² = 10² ; a = 6
C. Real-World Applications
- Distance Calculation: Explain how the theorem can be used to calculate distances (e.g., finding the length of a ramp, determining if a large screen TV will fit in an entertainment center).
- Construction: Describe how builders use the theorem to ensure right angles are accurate.
- Navigation: Mention how the theorem is used in navigation and surveying.
- Diagrammatic Representation: Whenever possible, accompany each application with a diagram to illustrate the scenario.
IV. Advanced Concepts (Optional)
This section could delve into more complex related topics, but is not strictly necessary.
A. Pythagorean Triples
- Definition: Explain what Pythagorean triples are (sets of three positive integers that satisfy the Pythagorean theorem).
- Common Examples: List common examples like (3, 4, 5), (5, 12, 13), and (8, 15, 17).
- Generating Triples: Briefly mention how to generate Pythagorean triples.
B. Converse of the Pythagorean Theorem
- Explanation: Explain that if the square of one side of a triangle equals the sum of the squares of the other two sides, then the triangle is a right triangle.
- Application: Show how this can be used to determine if a triangle is a right triangle when only the side lengths are known.
This structured approach ensures a comprehensive and easily digestible explanation of the relationship between the legs and hypotenuse of a right triangle, using the target keywords effectively throughout the article. The progressive nesting of headings allows readers to easily navigate to sections of interest.
Legs & Hypotenuse: Frequently Asked Questions
This FAQ aims to clarify common questions about right triangles, focusing on the concepts of legs and the hypotenuse.
What exactly are the "legs" of a right triangle?
The legs of a right triangle are the two sides that form the right angle (90 degrees). They are sometimes also called the "cathetus". The leg sides are opposite to the acute angles in the right triangle.
How do I identify the hypotenuse?
The hypotenuse is the longest side of a right triangle, and it’s always opposite the right angle. Another way to remember it is that the legs make up the right angle and the hypotenuse is always the side opposite the 90 degree angle.
Why are the legs and hypotenuse important?
The legs and hypotenuse are critical for understanding and applying the Pythagorean theorem (a² + b² = c²). This theorem lets you find the length of an unknown side if you know the length of the other two, either legs or hypotenuse.
Can a right triangle have two hypotenuses?
No, a right triangle can only have one hypotenuse. The hypotenuse is defined specifically as the side opposite the right angle, and right triangles only have one right angle. Therefore, there’s only one side that fits that definition.
So, there you have it! Hopefully, you now have a clearer picture of what’s going on with those ever-important legs and hypotenuse. Go forth and conquer those right triangles!