Hexagon Secrets: Unequal Sides, One Symmetry Line!
Geometry explores shapes, and symmetry is a fundamental property within this field. This article examines a specific case: the intriguing picture of hexagon with unequal sides with 1 line of symmetry. The mathematical principles governing such shapes dictate that specific angular and side-length relationships must exist to maintain this single axis of reflection. Exploring this concept, we will touch upon the application of Euclidean geometry, which provides the theoretical framework. Finally, understanding these shapes has practical relevance in fields like computer graphics, where algorithms often generate and manipulate asymmetric forms.
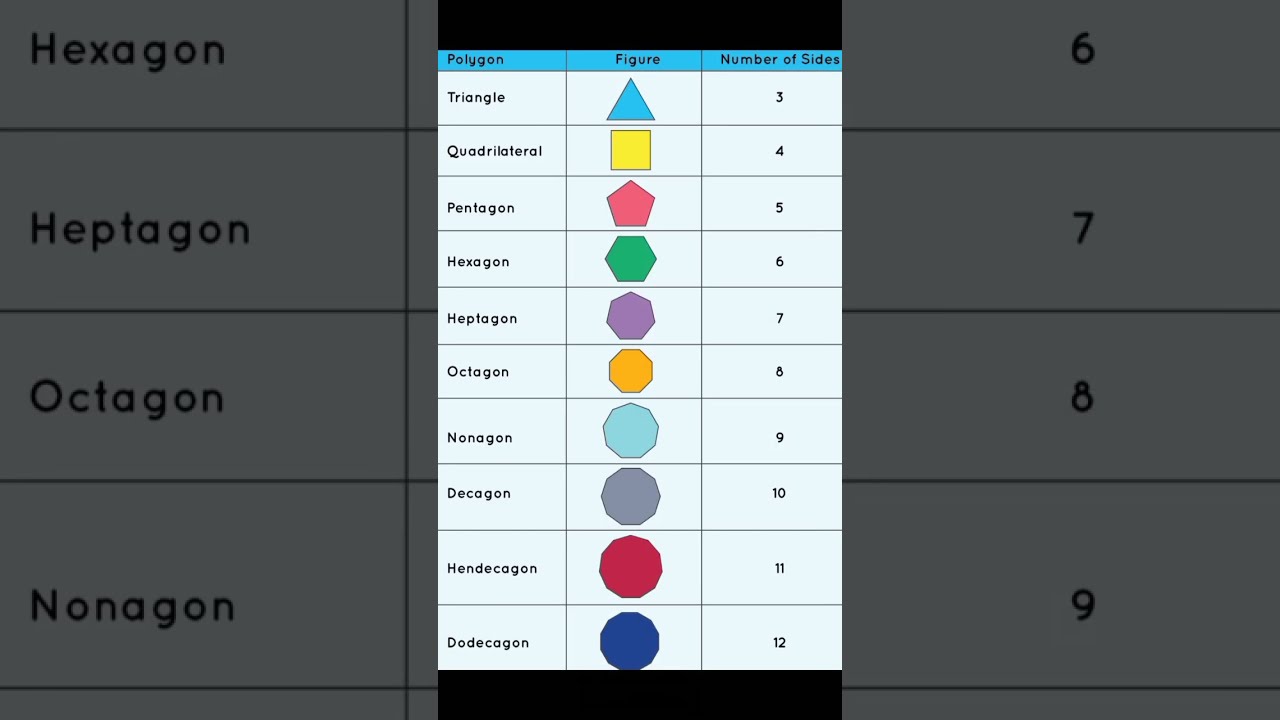
Image taken from the YouTube channel MATH CLUB , from the video titled Polygons with side up to 12 // 💁easy to remember // Math tricks 🔥 .
Exploring Asymmetrical Hexagons with Single-Axis Symmetry
A hexagon, by definition, is a six-sided polygon. While many envision hexagons with six equal sides and angles (regular hexagons), the realm of hexagons extends to those with unequal sides and angles. This exploration focuses on a specific subset: hexagons with unequal sides exhibiting only one line of symmetry. Critically, we need to visualize this concept, hence the importance of the phrase "picture of hexagon with unequal sides with 1 line of symmetry". This explanation will dissect the characteristics of such shapes and how to identify them.
Understanding Symmetry in Hexagons
Symmetry, in geometric terms, refers to a balanced and proportionate similarity found in two halves of an object. A line of symmetry (also known as an axis of symmetry) is an imaginary line that passes through the center of a shape, dividing it into two identical halves that are mirror images of each other.
Types of Symmetry
There are different types of symmetry, but in the context of this discussion, we are primarily concerned with reflectional symmetry (also called mirror symmetry or line symmetry).
Regular vs. Irregular Hexagons
- Regular Hexagon: Possesses six lines of symmetry. Three lines connect opposite vertices, and three lines bisect opposite sides. Additionally, they have rotational symmetry.
- Irregular Hexagon: Can have anywhere from zero to a maximum of six lines of symmetry, depending on the specific arrangement of its sides and angles. The focus of this discussion is a specific type of irregular hexagon.
Characteristics of a Hexagon with Unequal Sides and One Line of Symmetry
A hexagon with unequal sides and only one line of symmetry presents a unique geometric challenge. This configuration implies a specific arrangement of its sides and angles. If you imagine a "picture of hexagon with unequal sides with 1 line of symmetry," certain key characteristics become apparent:
- Paired Sides: Because there is one line of symmetry, at least two pairs of sides must be equal in length. These pairs are reflections of each other across the line of symmetry. The remaining two sides might be equal to each other or be completely different lengths.
- Paired Angles: Similarly, at least two pairs of angles must be equal. These pairs are also reflections of each other across the line of symmetry. The remaining two angles might be equal or different.
- Position of the Symmetry Line: The single line of symmetry either:
- Connects two opposite vertices (corners) of the hexagon.
- Bisects two opposite sides of the hexagon.
Visualizing the Hexagon
Understanding these characteristics is best achieved through visualization. Imagine or search for a "picture of hexagon with unequal sides with 1 line of symmetry." Observe the following details:
- Side Lengths: Note that not all six sides are the same length.
- Angle Measures: Observe that not all six angles are the same measure.
- Symmetry Axis: Pay close attention to the position of the single line of symmetry and how it divides the hexagon into two mirror images.
Examples
Here’s a conceptual example:
- Imagine a hexagon.
- Draw a vertical line down the middle. This is our line of symmetry.
- On the left side of the line, draw a side of length ‘a’ at a particular angle.
- Mirror this on the right side; draw a side of length ‘a’ at the reflected angle.
- Repeat with another side of length ‘b’.
- The remaining two sides can be of any length, as long as the overall figure remains a hexagon and the angles close properly.
Identifying Symmetry in a Hexagon with Unequal Sides
Given a hexagon with unequal sides, how do you determine if it has one line of symmetry?
- Visual Inspection: Look for any obvious lines that would divide the shape into mirror images. This requires careful observation. Referencing a "picture of hexagon with unequal sides with 1 line of symmetry" can help train your eye.
- Folding (Mentally or Physically): Imagine folding the hexagon along a potential line of symmetry. Do the two halves perfectly overlap? If so, that line is a line of symmetry.
- Measurement: If precise measurements of side lengths and angles are available, compare corresponding sides and angles on either side of a potential line of symmetry. If they are equal, that line is a line of symmetry.
- Testing with a Mirror: Place a mirror along a potential line of symmetry. If the reflection in the mirror, combined with the visible portion of the hexagon, creates a complete, identical hexagon, then that is a line of symmetry.
Hexagon Secrets: FAQs
This FAQ section answers common questions about hexagons with unequal sides and a single line of symmetry, as discussed in the article.
What exactly does "unequal sides" mean in this context?
It means that not all six sides of the hexagon are the same length. Unlike regular hexagons, where every side is identical, these hexagons have sides of varying lengths but still maintain a basic hexagonal shape.
How is it possible for a hexagon with unequal sides to have only one line of symmetry?
The line of symmetry perfectly divides the hexagon into two mirror-image halves. This is possible if the sides are arranged in a way that creates this reflective property, even if individual side lengths differ. A picture of hexagon with unequal sides with 1 line of symmetry illustrates how this arrangement works.
What are some real-world examples of hexagons with unequal sides and one line of symmetry?
While perfect examples are rare, many naturally occurring or human-made structures approximate this shape. For example, some crystals or tile patterns may feature hexagonal shapes with slightly irregular sides and a single axis of symmetry.
Can I easily draw a picture of hexagon with unequal sides with 1 line of symmetry?
Yes! Start by drawing the line of symmetry. Then, draw half of the hexagon on one side, ensuring that corresponding points on either side of the line are equidistant. Finally, mirror that half across the line to complete the hexagon.
So, there you have it! Hopefully, this shed some light on the fascinating world of a picture of hexagon with unequal sides with 1 line of symmetry. Go forth and explore other asymmetrical wonders!