Factorial Function: Real-World Applications You Won’t Believe!
The mathematical concept of the factorial function, often encountered in combinatorics, extends far beyond theoretical mathematics. Permutation calculations, a core component in probability theory, utilize factorials to determine the number of possible arrangements. Dr. Ada Lovelace, a pioneer in computer science, recognized the applications and mathematical significance of the factorial function in early computing contexts, particularly within analytical engines. Understanding these principles unlocks valuable insights in diverse fields, including optimizing delivery routes in logistics management.
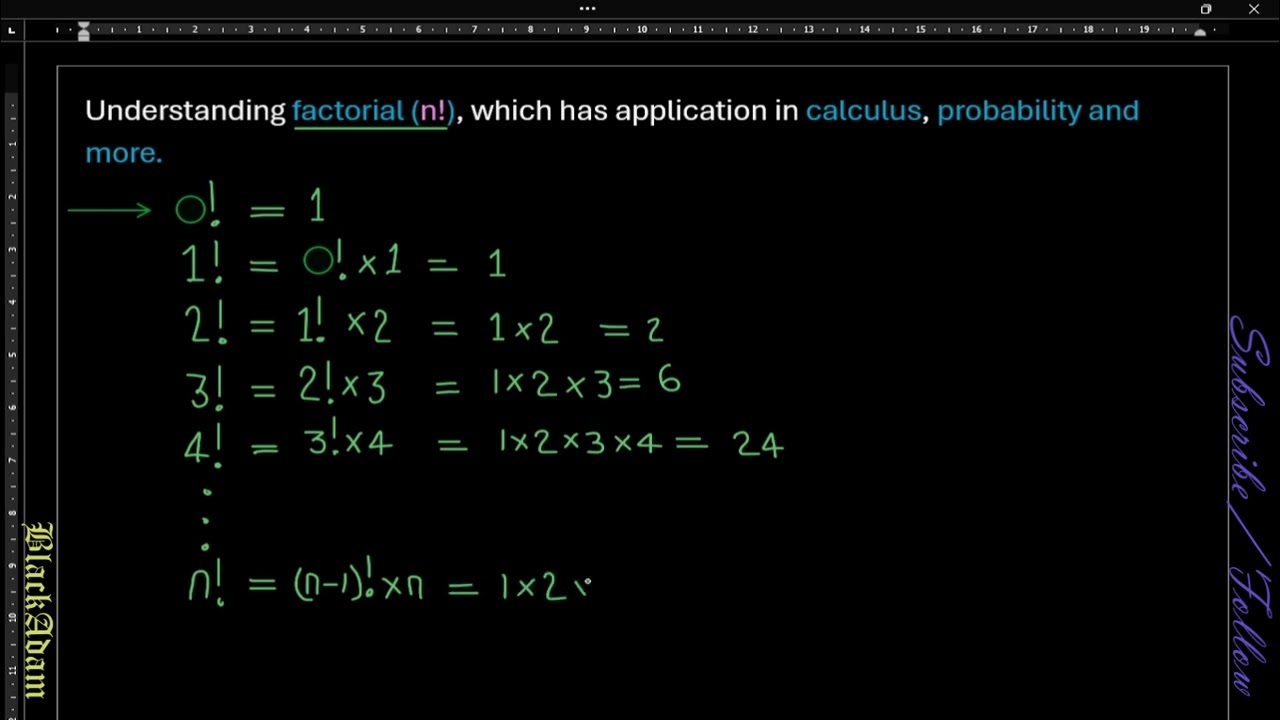
Image taken from the YouTube channel 5DTutor BlackAdam Math Physics and Chemistry Class , from the video titled Understanding Factorial which has application in Calculus, mathematical induction, probability, Comb .
The factorial function, denoted by n!, might initially appear as a simple mathematical curiosity. However, its influence extends far beyond the realm of pure mathematics, permeating fields as diverse as probability, statistics, and computer science. This seemingly unassuming function unlocks solutions to complex problems and provides a fundamental building block for understanding various phenomena.
Defining the Factorial Function
The factorial of a non-negative integer n, written as n!, is the product of all positive integers less than or equal to n. Mathematically, this is expressed as:
n! = n × (n-1) × (n-2) × … × 2 × 1
For example, 5! = 5 × 4 × 3 × 2 × 1 = 120. By convention, 0! is defined as 1. This definition is crucial for the consistency of various mathematical formulas and identities.
A Ubiquitous Mathematical Tool
The factorial function’s prevalence is often surprising to those encountering it for the first time. It arises naturally in scenarios involving permutations (arrangements) and combinations (selections), providing a powerful tool for counting the number of possible outcomes.
In probability theory, factorials are essential for calculating the likelihood of specific events, especially those involving ordered sequences or selections from a set.
Statisticians utilize factorials in various distributions and hypothesis tests, enabling them to analyze data and draw meaningful conclusions.
Computer scientists leverage factorials in the design and analysis of algorithms, particularly those related to sorting, searching, and optimization.
Thesis: Applications and Significance
This exploration delves into the significant applications and mathematical significance of the factorial function. It aims to demonstrate its utility across various domains. By examining its role in combinatorics, probability, statistics, and computer science, we uncover the profound impact of this fundamental mathematical concept. We highlight its versatility and enduring relevance in solving real-world problems and advancing scientific understanding.
The factorial function’s prevalence is often surprising to those encountering it for the first time. It arises naturally in scenarios involving permutations (arrangements) and combinations (selections), providing a powerful tool for counting the number of possible outcomes.
Decoding the Factorial: Definition, Calculation, and Core Properties
At its heart, the factorial function represents a fundamental concept in mathematics. It allows us to quantify the number of ways to arrange a set of distinct objects. Understanding its definition, calculation, and properties is crucial for appreciating its applications in various fields.
Defining and Calculating the Factorial
The factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n. In simpler terms, you multiply n by every positive integer smaller than it, down to 1.
Mathematically, this is expressed as:
n! = n × (n-1) × (n-2) × … × 2 × 1
For instance, to calculate 4!, we perform the following calculation:
4! = 4 × 3 × 2 × 1 = 24
This means there are 24 different ways to arrange 4 distinct objects.
By convention, 0! is defined as 1.
This seemingly arbitrary definition is essential for maintaining consistency in various mathematical formulas and combinatorial identities.
Key Mathematical Properties of Factorials
Recursive Nature
One of the most important properties of the factorial function is its recursive nature.
The factorial of n can be defined in terms of the factorial of n-1.
This recursive definition is expressed as:
n! = n × (n-1)!
This property is particularly useful in computer science for implementing factorial calculations using recursive algorithms.
Rapid Growth
The factorial function exhibits extremely rapid growth. As n increases, n! grows much faster than exponential functions.
For example, 5! = 120, while 10! = 3,628,800.
This rapid growth has implications for the computational complexity of algorithms involving factorials.
The Binomial Coefficient: A Factorial-Powered Tool
The binomial coefficient, often read as "n choose r", represents the number of ways to choose a subset of r elements from a set of n elements, without regard to order.
It is denoted as nCr or (nCr) and is calculated using factorials:
nCr = n! / (r! (n–r*)!)
The binomial coefficient is fundamental in probability, statistics, and combinatorics. It appears in various contexts, such as calculating the probabilities of events in coin flips or card games.
The factorial function forms the backbone of the binomial coefficient, providing the means to quantify combinations and selections. Its contribution is indispensable in scenarios involving counting possibilities without regard to order.
Factorials in Action: Mastering Permutations and Combinations
Having established the definition and core properties of factorials, we now turn our attention to their practical application. The true power of the factorial function shines in the realm of combinatorics, where it provides the essential toolkit for counting possibilities. Here, we’ll explore how factorials are indispensable for calculating permutations and combinations, two fundamental concepts in this field.
Permutations: The Art of Arrangement
Permutations deal with the number of ways to arrange objects in a specific order. The order of selection is paramount. Imagine you have a set of distinct items, and you want to know how many different ways you can line them up. This is a permutation problem.
The formula for calculating the number of permutations of r objects chosen from a set of n distinct objects is:
nPr = n! / (n-r)!
Here, n represents the total number of objects available, and r represents the number of objects we are arranging. The exclamation mark, of course, signifies the factorial operation.
Let’s illustrate this with an example. Suppose we have five distinct books (A, B, C, D, and E) and we want to arrange three of them on a shelf. How many different arrangements are possible?
Using the formula:
5P3 = 5! / (5-3)! = 5! / 2! = (5 × 4 × 3 × 2 × 1) / (2 × 1) = 60
Therefore, there are 60 different ways to arrange three books chosen from a set of five.
Combinations: The Science of Selection
In contrast to permutations, combinations are concerned with the number of ways to choose a subset of objects from a larger set, without regard to order. The order of selection does not matter. If you’re picking a group of people for a team, the order in which you choose them doesn’t change the composition of the team.
The formula for calculating the number of combinations of r objects chosen from a set of n distinct objects is:
nCr = n! / (r! * (n-r)!)
Notice the addition of r! in the denominator. This accounts for the fact that we are not concerned with the order in which the r objects are chosen.
Let’s consider an example. Suppose we have a group of seven people, and we want to form a committee of four. How many different committees can we form?
Using the formula:
7C4 = 7! / (4! (7-4)!) = 7! / (4! 3!) = (7 × 6 × 5 × 4 × 3 × 2 × 1) / ((4 × 3 × 2 × 1) × (3 × 2 × 1)) = 35
Thus, there are 35 different ways to form a committee of four from a group of seven people.
Real-World Illustrations: Bringing it all Together
To solidify these concepts, let’s consider some real-world examples.
Arranging Books (Permutations)
Imagine you have eight different books, and you want to arrange five of them on a shelf.
This is a permutation problem because the order in which the books are placed matters. The number of possible arrangements is 8P5 = 8! / (8-5)! = 8! / 3! = 6720.
Selecting a Committee (Combinations)
Suppose you need to select a committee of three people from a group of ten.
This is a combination problem because the order in which you choose the committee members does not matter. The number of possible committees is 10C3 = 10! / (3! (10-3)!) = 10! / (3! 7!) = 120.
By understanding the distinction between permutations and combinations, and mastering the factorial function, you gain a powerful tool for solving a wide range of counting problems that arise in various fields, from probability to computer science.
Having explored the world of permutations and combinations, and seen how factorials enable us to count arrangements and selections, we now turn our attention to another critical area where factorials play a vital role: probability and statistics. The ability to accurately calculate probabilities is essential in countless applications, from assessing risk in financial markets to predicting the outcome of scientific experiments. As we’ll see, factorials provide a powerful tool for unlocking these probabilities, especially when dealing with events involving ordered arrangements or selections from a finite set.
Probability and Statistics: Unlocking Probabilities with Factorials
The factorial function isn’t just a mathematical curiosity; it’s a foundational element in probability theory and statistical analysis. Its ability to count the number of possible outcomes in various scenarios makes it indispensable for calculating probabilities and understanding statistical distributions.
Calculating Probabilities with Factorials
Factorials shine when dealing with scenarios involving permutations and combinations, as previously discussed. Calculating the probability of specific events often requires determining the total number of possible outcomes and the number of outcomes that satisfy a particular condition.
Consider the probability of drawing specific cards in a particular order from a deck. This requires calculating the number of successful sequences (permutations) and dividing it by the total number of possible sequences.
The factorial function is essential for both of these calculations. Let’s look at a simple example.
What is the probability of drawing three specific cards in a specific order, without replacement, from a standard 52-card deck? The total number of ways to draw three cards in order is 52P3 = 52! / (52-3)! = 52 51 50. If we want to draw, say, the Ace of Spades, then the King of Hearts, and then the Queen of Diamonds, there is only one way to do that. Therefore, the probability is 1 / (52 51 50), which highlights the power of factorials in determining probabilities in such cases.
Factorials in Statistical Analysis
Beyond simple probability calculations, the factorial function is interwoven into various statistical formulas and distributions. It is a key component of both the Poisson and Binomial distributions.
Poisson Distribution
The Poisson distribution models the probability of a given number of events occurring in a fixed interval of time or space, given that these events occur with a known average rate and independently of the time since the last event.
The formula for the Poisson distribution involves the factorial function:
P(x; μ) = (e-μ) (μx) / x!
Where:
- P(x; μ) is the probability of observing x events.
- μ is the average rate of event occurrence.
- x! is the factorial of x.
- e is Euler’s number (approximately 2.71828).
Binomial Distribution
The binomial distribution models the probability of obtaining a certain number of successes in a fixed number of independent trials, each with the same probability of success.
The formula for the binomial distribution involves the factorial function through the binomial coefficient:
P(x; n, p) = (nCx) px (1-p)n-x = [n! / (x! (n-x)!)] px
**(1-p)n-x
Where:
- P(x; n, p) is the probability of observing x successes in n trials.
- n is the number of trials.
- p is the probability of success on a single trial.
- x is the number of successes.
- nCx is the binomial coefficient, calculated using factorials.
Lottery Example: A Real-World Application
A classic example of factorials in probability is calculating the odds of winning a lottery. Lotteries typically involve selecting a set of numbers from a larger pool, and the order of selection usually doesn’t matter.
Therefore, the number of possible outcomes is a combination, calculated using factorials. Consider a lottery where you must choose 6 numbers from a pool of 49. The total number of possible combinations is 49C6 = 49! / (6!** 43!) = 13,983,816.
This means the probability of winning with a single ticket is 1 in 13,983,816. The sheer scale of this number illustrates the power of combinatorial calculations, which rely heavily on the factorial function.
Factorials in Hypothesis Testing
Factorials also indirectly influence hypothesis testing through statistical distributions. Many test statistics (like chi-squared) rely on distributions which themselves are built upon factorial calculations, as shown previously. Therefore, the foundational understanding of factorials is essential for interpreting p-values and making informed decisions based on statistical evidence.
In conclusion, the factorial function is not merely a theoretical concept; it’s a practical tool with profound implications for probability and statistics. From calculating the likelihood of specific events to understanding complex statistical distributions, factorials provide a fundamental building block for analyzing data and making informed decisions in a world governed by chance.
Having explored the world of permutations and combinations, and seen how factorials enable us to count arrangements and selections, we now turn our attention to another critical area where factorials play a vital role: probability and statistics. The ability to accurately calculate probabilities is essential in countless applications, from assessing risk in financial markets to predicting the outcome of scientific experiments. As we’ll see, factorials provide a powerful tool for unlocking these probabilities, especially when dealing with events involving ordered arrangements or selections from a finite set.
Computer Science and Algorithm Design: The Power of Factorials
The factorial function may seem like a purely mathematical concept, but it has profound implications in computer science. Its influence permeates the design and analysis of algorithms, especially those dealing with combinatorial problems. Understanding factorials is crucial for assessing algorithm efficiency and determining their suitability for various computational tasks.
Factorials in Algorithm Design and Analysis
Factorials play a significant role in the analysis and design of algorithms, particularly those that involve generating permutations or combinations. When an algorithm needs to explore all possible arrangements or subsets of a dataset, the number of operations often scales factorially.
For instance, consider a brute-force algorithm that attempts to find the optimal solution by exhaustively checking every possibility. If the number of possibilities is related to a factorial, the algorithm’s performance will degrade rapidly as the input size increases.
Sorting algorithms that explore different permutations to find the correct order of elements are also influenced by factorial considerations.
Although most efficient sorting algorithms (e.g., merge sort, quicksort) avoid explicitly generating all permutations, understanding the factorial complexity helps appreciate the improvement offered by these optimized approaches.
Big O Notation and Factorial Complexity
In computer science, Big O notation is used to describe the asymptotic behavior of an algorithm, i.e., how its runtime or memory usage grows as the input size grows. The factorial function frequently appears in Big O notation to represent the time complexity of certain algorithms.
An algorithm with a time complexity of O(n!) indicates that the number of operations it performs grows proportionally to the factorial of the input size n. Such algorithms are generally considered impractical for large input sizes due to their exponential growth.
Algorithms with factorial time complexity are often associated with problems where every possible arrangement or combination needs to be evaluated. While such brute-force approaches may be suitable for small datasets, they quickly become infeasible as the input size increases.
Therefore, recognizing factorial complexity in Big O notation is vital for understanding the limitations of certain algorithms and motivates the search for more efficient solutions.
Example: The Traveling Salesperson Problem
The Traveling Salesperson Problem (TSP) is a classic example that showcases the impact of factorials on algorithm complexity. Given a list of cities and the distances between them, the TSP aims to find the shortest possible route that visits each city exactly once and returns to the starting city.
A brute-force approach to solving the TSP involves generating all possible permutations of the cities and calculating the total distance for each route. With n cities, there are (n-1)! possible routes to consider (since the starting city is fixed).
Therefore, the time complexity of this brute-force algorithm is O(n!). As the number of cities increases, the computational cost grows factorially, quickly exceeding the capabilities of even the most powerful computers.
For example, with just 20 cities, there are approximately 1.2 x 1017 possible routes, rendering a brute-force solution completely impractical. This illustrates the limitations of algorithms with factorial complexity and highlights the need for more sophisticated approaches, such as heuristics and approximation algorithms, to tackle the TSP for larger instances.
Beyond the Basics: Advanced Mathematical Concepts and Factorials
Having witnessed the factorial function’s versatility in tackling permutations, combinations, probabilities, and even influencing algorithm design, it’s time to venture beyond the fundamentals. The factorial, while powerful in its own right, serves as a springboard into more advanced mathematical concepts, particularly when dealing with extremely large numbers or extending its definition to a broader domain. These advanced concepts not only enhance our understanding of the factorial itself but also provide invaluable tools for approximation and generalization.
Stirling’s Approximation: Taming the Factorial Beast
Calculating the factorial of even moderately sized numbers can quickly become computationally expensive. For instance, 20! is already a substantial number, and calculating factorials for values in the hundreds or thousands poses a significant challenge. Stirling’s approximation offers a powerful solution to this problem.
It provides an approximate formula for calculating the factorial of large numbers, circumventing the need for direct, iterative multiplication. This approximation is invaluable in situations where an exact factorial value is unnecessary, or where the number is simply too large for direct computation.
The formula for Stirling’s approximation is:
n! ≈ √(2πn)
**(n/e)^n
Where:
- π (pi) is approximately 3.14159
- e is Euler’s number, approximately 2.71828
This formula reveals a fascinating connection between the factorial function, continuous functions like the square root and exponential functions, and fundamental mathematical constants.
Stirling’s approximation becomes increasingly accurate as n grows larger. It’s a cornerstone in various fields, including statistical mechanics and probability theory, where dealing with enormous factorials is commonplace.
Significance of Stirling’s Approximation
The significance of Stirling’s approximation lies in its ability to transform a computationally intensive factorial calculation into a relatively simple algebraic expression. This makes it possible to analyze and understand the behavior of systems involving large combinatorial quantities.
For example, in statistical mechanics, calculating the number of possible microstates of a system often involves extremely large factorials. Stirling’s approximation allows physicists to sidestep the computational bottleneck and derive meaningful results.
The Gamma Function: Extending the Factorial
The factorial function is initially defined only for non-negative integers. The Gamma function, denoted by Γ(z), provides a remarkable generalization of the factorial function to complex numbers (except for non-positive integers).
It offers a continuous interpolation of the factorial, extending its domain beyond the discrete set of integers. This extension opens up new avenues for analysis and application in various branches of mathematics, physics, and engineering.
The Gamma function is defined by the integral:
Γ(z) = ∫0^∞ t^(z-1)** e^(-t) dt
For positive integers, the Gamma function is related to the factorial function by the simple equation:
Γ(n) = (n-1)!
This relationship highlights the Gamma function as a true generalization of the factorial. It smoothly connects the discrete factorial values at integer points, creating a continuous function that captures the essence of the factorial concept.
The Gamma Function and the Factorial Function
The Gamma function’s seamless integration with the factorial function offers powerful analytical tools. By allowing factorial-like calculations for non-integer values, the Gamma function enables solutions to problems that would be intractable using the standard factorial definition alone.
It appears in various integral formulas, special functions, and differential equations, demonstrating its profound influence across different mathematical domains.
Example: Approximating Factorials with Stirling’s Formula
Let’s illustrate the power of Stirling’s approximation by estimating 100!
Using Stirling’s formula:
100! ≈ √(2π 100) (100/e)^100
100! ≈ √(200π)
**(100/2.71828)^100
100! ≈ 25.066** (36.788)^100
100! ≈ 9.33 x 10^157
The actual value of 100! is approximately 9.332621544 × 10^157. As you can see, Stirling’s approximation provides a remarkably accurate estimate, even for a number as relatively small as 100.
This example demonstrates the practical utility of Stirling’s approximation in dealing with large factorials. It allows us to quickly obtain a reasonable estimate without performing the tedious and computationally expensive direct calculation.
Applications Across Disciplines: Real-World Examples
Having explored the intricacies of Stirling’s approximation and glimpsed the elegance of the Gamma function, it’s beneficial to consolidate our understanding by revisiting how the factorial function manifests across diverse disciplines. This section will draw upon examples previously discussed to showcase the broad applicability and practical significance of this fundamental mathematical concept.
Combinatorics and the Arrangement of Possibilities
The factorial function’s presence is undeniable in combinatorics, the branch of mathematics concerned with counting. Consider the problem of arranging n distinct objects. The factorial, n!, directly quantifies the number of possible permutations.
This seemingly simple concept underpins many real-world scenarios. Think of scheduling tasks, assigning employees to projects, or even arranging the order in which you tackle your daily chores. Each arrangement represents a distinct permutation, and the factorial function provides the tool to enumerate these possibilities efficiently.
Probability and the Quantification of Chance
The factorial function also features prominently in probability calculations, especially when dealing with combinations and permutations. When calculating the likelihood of specific events occurring in a particular order (permutations) or the probability of selecting a specific subset from a larger group (combinations), the factorial function is indispensable.
For example, determining the odds of winning a lottery involves calculating the number of possible combinations of numbers, a computation that relies directly on the factorial function. Similarly, statistical analysis leverages the factorial function in various formulas and distributions, such as the Poisson and binomial distributions, to model and understand random phenomena.
Algorithm Design and Computational Complexity
In computer science, the factorial function’s influence extends to algorithm design and analysis. While algorithms with factorial time complexity (O(n!)) are generally avoided due to their rapid growth, understanding this complexity class is crucial.
For instance, brute-force approaches to solving problems like the Traveling Salesperson Problem (TSP) often involve examining all possible routes, leading to a factorial time complexity. Although impractical for large problem instances, these examples highlight the factorial function’s role in characterizing the computational demands of certain algorithms.
Discrete Mathematics and Network Analysis
Beyond these core areas, the factorial function finds applications in more specialized domains. Discrete mathematics, a foundational area for computer science, utilizes the factorial function in graph theory and network analysis.
Problems related to counting paths within a network, determining the number of possible arrangements of nodes, or analyzing the connectivity of a graph often involve factorial calculations. These applications demonstrate the enduring relevance of the factorial function in both theoretical and applied contexts.
In conclusion, while the factorial function may appear abstract, its applications are widespread and profound. From calculating probabilities to analyzing algorithms, the factorial function provides a powerful tool for understanding and solving problems across a multitude of disciplines.
FAQs: Factorial Function and Its Surprising Uses
Still curious about factorials? Here are some frequently asked questions to further explore the fascinating applications and mathematical significance of the factorial function.
What exactly is a factorial?
A factorial, denoted by n!, is the product of all positive integers less than or equal to n. For example, 5! = 5 4 3 2 1 = 120. It’s a fundamental concept in combinatorics and probability.
Beyond permutations, where else is the factorial function used?
While permutations are a key application, factorials also appear in probability calculations, statistical mechanics (counting arrangements of particles), and even in some advanced calculus formulas. The breadth of these applications highlights its mathematical significance.
How does the factorial function relate to probability?
The factorial function is crucial in calculating probabilities, especially when dealing with combinations and permutations. It helps determine the total number of possible outcomes, a key element in determining the likelihood of a specific event. This is a significant application of the factorial function.
Why is 0! defined as 1?
Defining 0! as 1 might seem odd, but it maintains mathematical consistency. It allows formulas involving factorials to work correctly, particularly in combinatorics and binomial theorem applications. This definition ensures the ongoing mathematical significance of the factorial function.
So, there you have it – a peek into the surprising real-world applications and mathematical significance of the factorial function! Hopefully, you found something new and interesting. Now go forth and put those factorials to good use!