Unlock Circle Area: Central Angle Formula Secrets! 🔥
The concept of sector area, often visualized through geometrical tools like GeoGebra, presents a crucial foundation for understanding the area of circle with central angle formula. Many geometrical problems can be solved by area of circle with central angle formula. The application of trigonometry to calculate sector area has been studied extensively by mathematicians at institutions like Cambridge University. Finally, the calculation of sector area using the central angle is a core skill tested in many math competions.
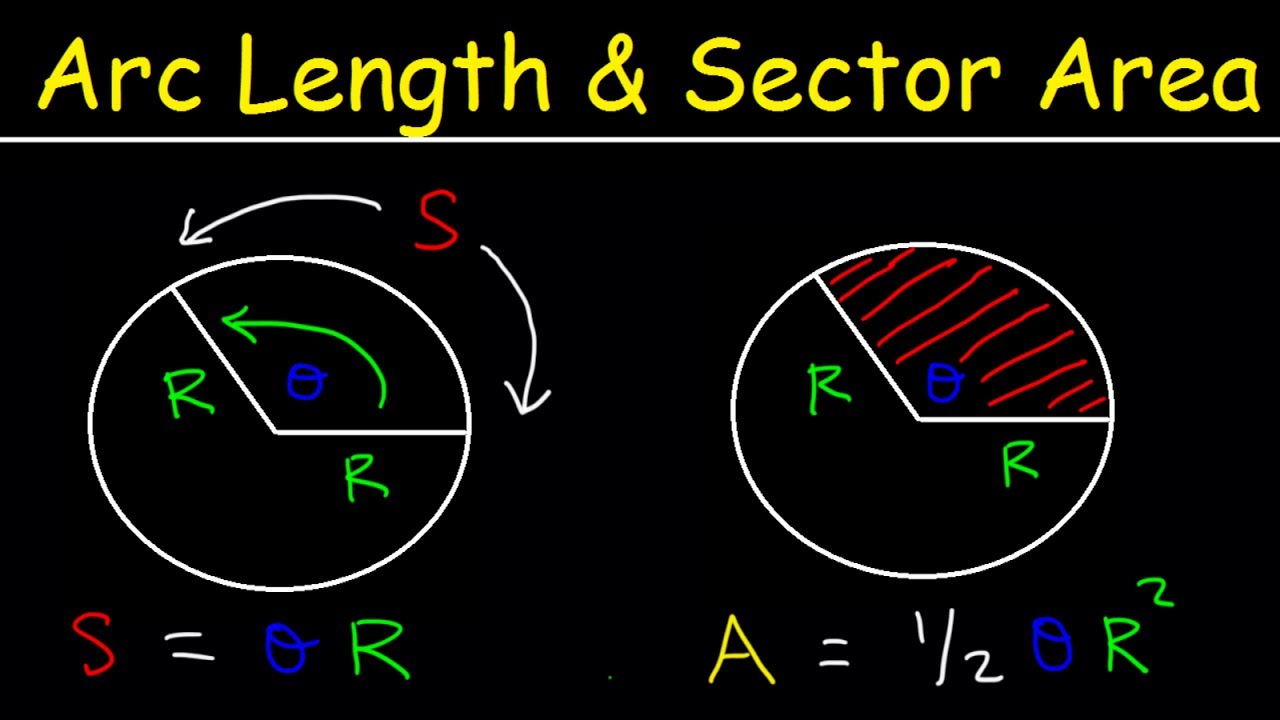
Image taken from the YouTube channel The Organic Chemistry Tutor , from the video titled Arc Length of a Circle Formula – Sector Area, Examples, Radians, In Terms of Pi, Trigonometry .
Imagine you’re designing a sprinkler system for a circular garden. You need to know how much area each sprinkler head will cover, not just the entire garden’s area. Or perhaps you’re calculating the amount of pizza in a slice – a real-world problem we can all appreciate. In both cases, understanding how to calculate the area of a circular sector, defined by a central angle, is crucial.
A circle, at its core, is a set of points equidistant from a central point. This distance is, of course, the radius. From this simple definition springs forth a world of geometric relationships. The diameter stretches across the circle through the center, twice the length of the radius. The circumference marks the distance around the circle.
Defining the Central Angle
The central angle is an angle whose vertex lies at the center of the circle. Its sides are radii of the circle. It’s measured in two primary units: degrees (where a full circle is 360°) and radians (where a full circle is 2π). The central angle carves out a specific arc length along the circumference and encloses a sector of the circle. This sector is a "slice" of the circle, bounded by the arc and the two radii forming the central angle.
Thesis Statement
This article will delve into the area of a circle with central angle formula, a powerful tool for calculating the area of a sector. We will explore its derivation, practical applications through examples, and its broader significance in geometry and mathematics. Through a careful and detailed examination, we aim to empower you with the knowledge and skills necessary to confidently calculate sector areas and understand their underlying principles.
Imagine you’re designing a sprinkler system for a circular garden. You need to know how much area each sprinkler head will cover, not just the entire garden’s area. Or perhaps you’re calculating the amount of pizza in a slice – a real-world problem we can all appreciate. In both cases, understanding how to calculate the area of a circular sector, defined by a central angle, is crucial.
A circle, at its core, is a set of points equidistant from a central point. This distance is, of course, the radius. From this simple definition springs forth a world of geometric relationships. The diameter stretches across the circle through the center, twice the length of the radius. The circumference marks the distance around the circle.
Defining the Central Angle
The central angle is an angle whose vertex lies at the center of the circle. Its sides are radii of the circle. It’s measured in two primary units: degrees (where a full circle is 360°) and radians (where a full circle is 2π). The central angle carves out a specific arc length along the circumference and encloses a sector of the circle. This sector is a "slice" of the circle, bounded by the arc and the two radii forming the central angle.
With a solid grasp of these fundamental concepts, we can now turn our attention to the crucial underpinnings that will allow us to navigate the central topic of area calculations.
Understanding Circle Fundamentals: Area and Central Angles
Before diving into the specifics of calculating the area of a circle with a central angle, let’s solidify our understanding of the foundational elements that define a circle and its properties. This will provide a solid base upon which to build our knowledge.
Core Components of a Circle
At the heart of every circle lies the center, the point from which all points on the circle are equidistant.
The radius is the distance from the center to any point on the circle.
The diameter is a line segment that passes through the center of the circle and connects two points on the circle; its length is twice the radius.
The circumference is the distance around the circle. It’s calculated using the formula C = 2πr, where r is the radius.
These four components are the bedrock of understanding circles and their related calculations.
Defining Area in the Context of a Circle
Area, in general terms, refers to the amount of two-dimensional space enclosed within a boundary.
In the case of a circle, the area represents the entire region contained within the circumference.
The formula for the area of a full circle is A = πr², where r is the radius. This formula gives us the total space within the circle’s boundary.
Understanding this concept of area as enclosed space is crucial when we move to discussing sectors of circles.
Thorough Explanation of Central Angles and Arc Length
The central angle is an angle whose vertex is located at the center of the circle. Its sides are formed by two radii that extend from the center to the circle’s circumference.
Central angles are measured in two primary units: degrees and radians. A full circle encompasses 360 degrees or 2π radians.
The arc length is the distance along the circumference of the circle intercepted by the central angle. It’s essentially a portion of the circle’s circumference.
The arc length (s) is related to the central angle (θ in radians) and the radius (r) by the formula s = rθ. This relationship is a cornerstone of understanding how central angles relate to the circle’s perimeter.
With a solid grasp of these fundamental concepts, we can now turn our attention to the crucial underpinnings that will allow us to navigate the central topic of area calculations.
Deriving the Area of Circle with Central Angle Formula
At this point, we’re ready to get into the heart of the matter. Here, we’ll break down how the formula for the area of a circle with a central angle is derived and understood.
This section aims to equip you with the knowledge to calculate the area of any circular sector, regardless of whether the central angle is given in degrees or radians.
The Foundation: Area of a Full Circle
Let’s begin by revisiting the foundational formula for the area of a full circle:
A = πr²
Where:
- A represents the area of the circle.
- π (pi) is a mathematical constant approximately equal to 3.14159.
- r is the radius of the circle.
This formula gives us the total area enclosed within the circle’s boundary.
Defining the Circular Sector
A sector of a circle is a portion of the circle enclosed by two radii and the arc intercepted between them. Imagine slicing a pizza; each slice represents a sector of the circular pizza.
The size of the sector is determined by the central angle formed by the two radii.
A larger central angle corresponds to a larger sector, and consequently, a greater area.
Area and the Central Angle: A Proportional Relationship
The key to finding the area of a sector lies in understanding the proportional relationship between the sector’s area and the central angle.
The area of a sector is directly proportional to the central angle it subtends.
In other words, if you double the central angle, you double the area of the sector.
This proportional relationship allows us to derive a formula for the area of a sector based on the central angle and the circle’s radius.
Derivation: Area of a Sector (Degrees)
When the central angle is measured in degrees, we can express the area of the sector as a fraction of the total area of the circle.
Here’s the step-by-step derivation:
-
The ratio of the sector’s central angle (θ) to the total angle of a circle (360°) represents the fraction of the circle that the sector occupies: θ/360°
-
Multiply this fraction by the total area of the circle (πr²) to obtain the area of the sector:
Area = (θ/360°) πr²**
Therefore, the formula for the area of a sector with a central angle θ in degrees is:
**Area = (θ/360°) πr²
Derivation: Area of a Sector (Radians)
When the central angle is measured in radians, the derivation is slightly different, but conceptually similar.
Here’s the breakdown:
-
The ratio of the sector’s central angle (θ) to the total angle of a circle (2π radians) represents the fraction of the circle that the sector occupies: θ/2π
-
Multiply this fraction by the total area of the circle (πr²) to obtain the area of the sector:
Area = (θ/2π) πr²**
-
Simplify the expression by cancelling out π: Area = (θ/2) r²**
Therefore, the formula for the area of a sector with a central angle θ in radians is:
*Area = (θ/2) r²
Practical Applications: Solving for Sector Area
The true test of any formula lies in its application. Theory must translate into practice. Here, we’ll put our knowledge of the area of a circle with a central angle to work through several examples. Each one will demonstrate a unique facet of the formula and build your confidence in solving sector-related problems. We’ll explore examples working with degrees, radians, solving for the angle itself, and calculating arc length.
Example 1: Calculating Sector Area with Degrees
Consider a circle with a radius of 8 cm. A sector within this circle is defined by a central angle of 60°. Our goal is to determine the area of this sector.
Using the formula: Area = (θ/360°)
**πr², where θ is the central angle in degrees, we have:
Area = (60°/360°) π (8 cm)²
Area = (1/6) π 64 cm²
Area ≈ 33.51 cm²
Therefore, the area of the sector is approximately 33.51 square centimeters. This example highlights the direct application of the formula when the central angle is provided in degrees.
Example 2: Calculating Sector Area with Radians
Now, let’s tackle a scenario where the central angle is given in radians. Suppose we have a circle with a radius of 5 inches and a sector defined by a central angle of π/4 radians.
The formula for the area of a sector with the central angle in radians is: Area = (θ/2)** r².
Plugging in the values:
Area = (π/4 / 2) (5 inches)²
Area = (π/8) 25 inches²
Area ≈ 9.82 inches²
Thus, the area of the sector is approximately 9.82 square inches. This demonstrates the efficiency of the radian-based formula when dealing with angles expressed in radians.
Example 3: Solving for the Central Angle
What if we know the area of a sector and the radius of the circle, but we need to find the central angle? This is where rearranging the formula comes in handy.
Let’s say a sector has an area of 20 cm² within a circle of radius 6 cm. We’ll use the radian formula, as it’s generally simpler to work with.
Area = (θ/2)
**r²
Rearranging for θ: θ = (2** Area) / r²
Plugging in our values: θ = (2
**20 cm²) / (6 cm)²
θ = 40 / 36
θ ≈ 1.11 radians
Therefore, the central angle is approximately 1.11 radians. This example showcases the versatility of the formula beyond simply calculating the sector’s area. Being able to manipulate the formula is a crucial skill.
Example 4: Arc Length Calculation
The area of a sector is intrinsically linked to the arc length it subtends. Let’s explore a problem where we calculate the arc length.
Suppose a circle has a radius of 10 meters, and a sector within this circle has a central angle of 3π/5 radians. The formula for arc length (s) is: s = rθ
Plugging in the values: s = 10 meters** (3π/5)
s = 6π meters
s ≈ 18.85 meters
Therefore, the arc length of the sector is approximately 18.85 meters. This example illustrates the connection between central angles, radius, and arc length, further enriching our understanding of circular geometry. Remember, arc length is the distance along the curve of the sector.
Practical examples and problem-solving unlock the formula’s potential, but understanding its broader impact solidifies its place in mathematics. Let’s explore why calculating the area of a circle with a central angle is more than just a geometric exercise; it’s a fundamental tool with far-reaching implications.
Significance in Geometry and Mathematics
The formula for calculating the area of a circle with a central angle isn’t an isolated concept. It’s a cornerstone that supports numerous geometric and mathematical principles. Its importance stems from its ability to bridge fundamental concepts to more advanced applications.
A Foundation in Geometric Calculations
At its core, the area of a circle with a central angle formula provides a precise method for determining a portion of a circle’s area. This is crucial for various geometric calculations:
-
Sector Analysis: Understanding the area of a sector allows for accurate measurement and comparison of different sections within a circle.
-
Geometric Proofs: The formula can be used as a building block in more complex geometric proofs and derivations.
-
Shape Decomposition: Complex shapes can be broken down into simpler components, including circular sectors, to calculate their total area.
The ability to accurately calculate sector areas is paramount for architects, engineers, and designers.
Relevance in Advanced Mathematics
Beyond basic geometry, the area of a circle with a central angle plays a vital role in advanced mathematical concepts.
-
Calculus (Integration): The concept is fundamental to understanding integration in polar coordinates, where areas are calculated by summing infinitesimal sectors.
-
Trigonometry: The relationship between central angles and arc length, and subsequently sector area, is intimately linked to trigonometric functions.
-
Complex Analysis: Sectors and central angles are used when visualizing and understanding complex numbers in the complex plane, especially in concepts like roots of unity and conformal mappings.
-
Differential Geometry: The principles extend into the study of curves and surfaces, especially when dealing with curvature and area calculations on curved spaces.
-
Statistics and Probability: Circular distributions and angular data often rely on understanding proportions of circular areas defined by central angles.
The formula provides a foundational understanding upon which these advanced concepts are built.
Real-World Applications
The applications of this formula extend far beyond the classroom.
-
Engineering: Calculating the surface area of curved structures, designing gears and rotating components, and analyzing stress distributions in circular objects all rely on this principle.
-
Architecture: Designing curved facades, calculating material requirements for domes and arches, and optimizing the use of space in circular layouts.
-
Manufacturing: Calculating the area of circular cutouts in materials, determining the amount of coating needed for circular products, and ensuring precision in machining circular parts.
-
Navigation: Determining distances on maps using the relationship between central angles and arc length.
-
Computer Graphics: Rendering circular shapes and calculating areas for collision detection and other graphical operations.
-
Astronomy: Calculating the visible area of celestial bodies, understanding the geometry of orbits, and analyzing the distribution of matter in circular patterns.
From designing efficient gears to mapping the cosmos, the area of a circle with a central angle is an indispensable tool for solving real-world problems. Its versatility and fundamental nature make it a vital concept for anyone studying or working in a STEM field.
Practical examples and problem-solving unlock the formula’s potential, but understanding its broader impact solidifies its place in mathematics. Now, let’s shift our focus to ensuring the accuracy of our calculations. Avoiding common pitfalls is just as crucial as understanding the formula itself. A seemingly small error in units or measurements can lead to significant discrepancies in the final result. Let’s highlight some critical accuracy tips.
Avoiding Common Pitfalls: Accuracy Tips
The formula for the area of a circle with a central angle is relatively straightforward.
However, its correct application hinges on paying close attention to detail.
Neglecting seemingly minor aspects can lead to substantial errors, undermining the validity of your calculations.
Let’s explore some common pitfalls and practical tips to avoid them.
The Crucial Distinction: Degrees vs. Radians
One of the most frequent errors arises from using the incorrect angular unit.
The area formula changes depending on whether the central angle (θ) is measured in degrees or radians.
- Degrees: Area = (θ/360°)
**πr²
- Radians: Area = (θ/2)** r²
Failing to recognize this distinction will inevitably lead to an incorrect answer.
Recommendation: Before plugging any values into the formula, double-check whether the angle is given in degrees or radians.
If necessary, convert the angle to the appropriate unit using the following conversion factors:
- Degrees to Radians: radians = (degrees
**π) / 180
- Radians to Degrees: degrees = (radians** 180) / π
Always explicitly state the unit of measurement alongside the numerical value of the angle to avoid ambiguity.
Radius vs. Diameter: Know the Difference
Another common source of error lies in confusing the radius (r) with the diameter (d) of the circle.
Remember that the radius is the distance from the center of the circle to any point on its circumference.
The diameter, on the other hand, is the distance across the circle passing through the center.
Importantly, the diameter is always twice the length of the radius (d = 2r).
If a problem provides the diameter, be sure to divide it by 2 to obtain the radius before using it in the area formula.
Using the diameter instead of the radius will result in a fourfold error in the area calculation, emphasizing the importance of this distinction.
Understanding Proportionality
The area of a sector is directly proportional to the central angle.
This means that if you double the central angle, you double the area of the sector (assuming the radius remains constant).
Similarly, halving the central angle will halve the area.
However, it is also important to remember that the area is proportional to the square of the radius.
If you double the radius, you quadruple the area of the sector (again, assuming the angle remains constant).
Avoiding Misinterpretations
A common misconception is that a small change in the central angle or radius will result in a similarly small change in the area.
While this might be true for extremely small changes, the non-linear relationship between the radius and area means that even moderate changes in the radius can significantly impact the final result.
Always carefully consider the magnitudes of both the central angle and the radius when estimating or interpreting the area of a sector.
FAQs About Circle Area and Central Angles
Got questions about calculating circle areas using central angles? Here are some common questions answered to help you understand the concept better.
What exactly is a central angle?
A central angle is an angle whose vertex (the point where the two lines meet) is at the center of a circle, and its sides intersect the circle.
How does a central angle relate to calculating the area of a circle with central angle formula?
When you know the central angle and the radius of the circle, you can calculate a sector of the circle. The area of circle with central angle formula involves calculating the area of that sector.
What is the formula for calculating the area of a circle with central angle formula?
The area of a sector (a portion of a circle defined by a central angle) is calculated using this formula: Area = (central angle / 360°) * πr², where ‘r’ is the radius of the circle and the central angle is measured in degrees.
What if the central angle is given in radians?
If the central angle is given in radians, the formula changes slightly. The area of circle with central angle formula in radians is: Area = (1/2) r² θ, where ‘r’ is the radius and ‘θ’ is the central angle in radians.
And there you have it! Hopefully, you now have a much better grasp of the area of circle with central angle formula and can tackle those tricky problems with confidence. Go give it a try!